Topology 02 - Metric spaces : taking continuity beyond the real line

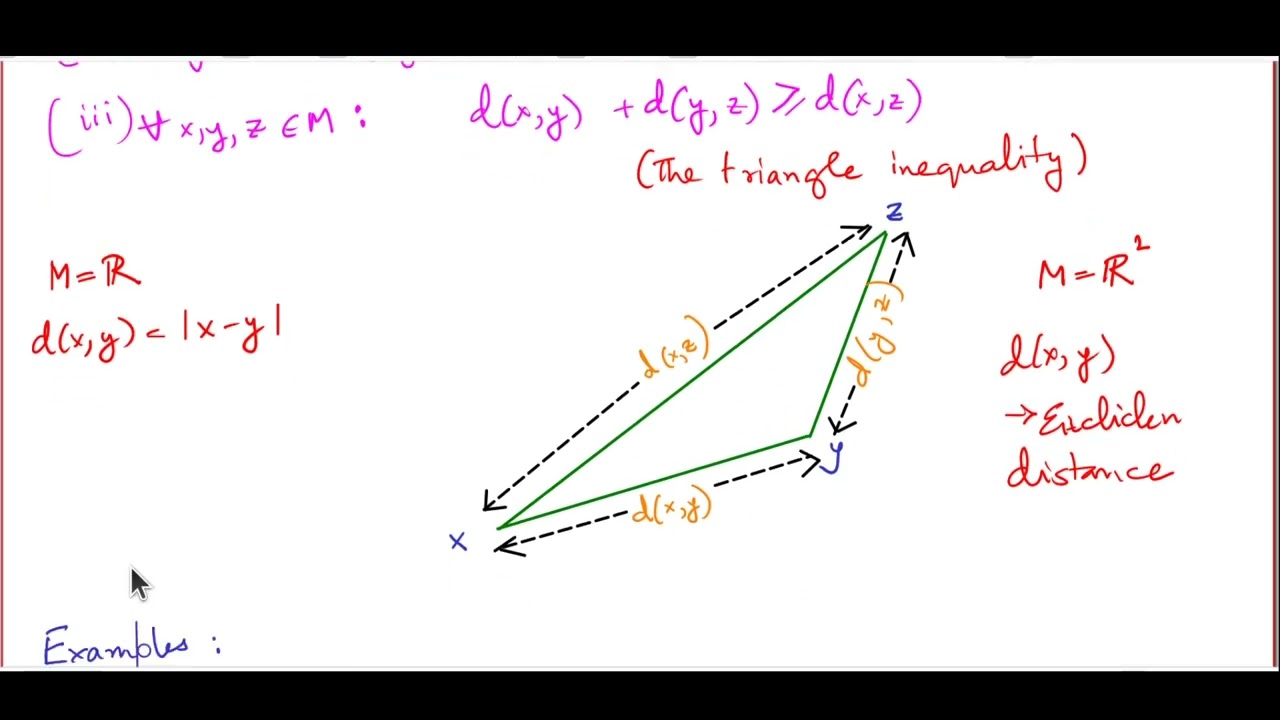
In this lecture I discuss the idea of metric spaces, sets in which a special structure - the metric function - is available, which allows us to talk of the distance between any two of its elements. After recapitulating the definition of metric spaces - I look at several examples. I then recount how the definition of continuity of functions on the real line generalises to metric spaces. I then proceed to define the fundamental building blocks on metric spaces - the open balls, and go on to see how we can rewrite our definition of continuity in the language of open balls. I then discuss how the open balls allow us to compare different metrics and describe the conditions under which we can treat two metrics as equivalent. I then define open sets and describe how the open sets that a metric describes end up up being more important than the precise form of the metric function itself. This will pave the way to our final goal - the ability to discuss continuity even in spaces where the notion of distance does not make sense.