Olympiad Geometry Problem #49: Cyclic Quad, Perpendiculars

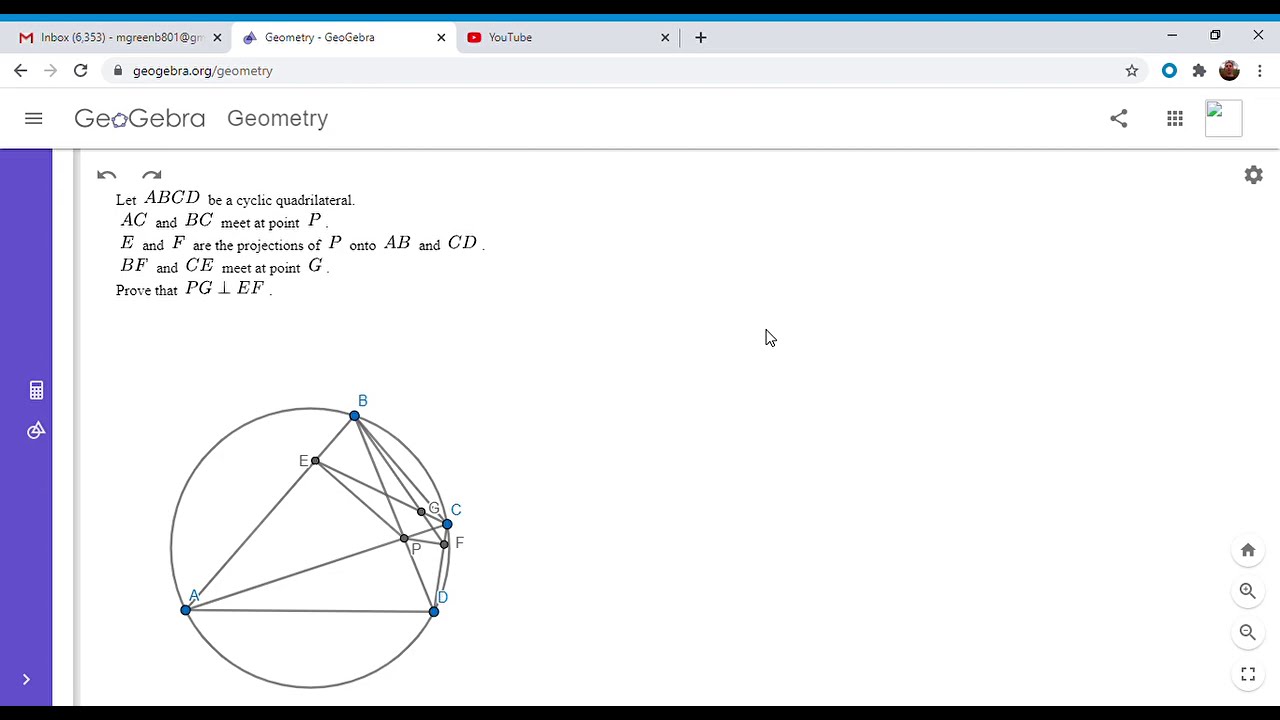
preview_player
Показать описание
This is a very elegant problem from the 2012 USA Team Selection Test for the IMO. It was posted by Evan Chen on the Art of Problem Solving Forum. Enjoy! Links below.
  1. Michael Greenberg
Рекомендации по теме
Olympiad Geometry Problem 0:12:05

Olympiad Geometry Problem #49: Cyclic Quad, Perpendiculars

Olympiad Geometry Problem 0:13:43

Olympiad Geometry Problem #50: Incenter, Midpoint, Parallel

Olympiad Geometry Problem 0:16:00

Olympiad Geometry Problem #48: Gauss Line

Olympiad Geometry Problem 0:12:26

Olympiad Geometry Problem #93: Two Isosceles Triangles, Circumcircle, Perpendicular

MATH OLYMPIAD. A 0:04:49

MATH OLYMPIAD. A nice solution on CIRCLE GEOMETRY

NEWYES Calculator VS 0:00:14

NEWYES Calculator VS Casio calculator

India vs japan 0:00:12

India vs japan || mathematics challenge || 😅🤣🤣🤭

When mathematicians get 0:00:37

When mathematicians get bored (ep1)

IMO 1985 Problem 0:02:58

IMO 1985 Problem 1: An Easiest Geometry Problem

Olympiad Geometry Problem 0:08:42

Olympiad Geometry Problem #43: IMO 2017 #4

Olympiad Geometry Problem 0:05:46

Olympiad Geometry Problem #69: Tangents, Secant, Perpendicular

Olympiad Geometry Problem 0:09:30

Olympiad Geometry Problem #98: Circumcenter, Midpoints, Equal Angle

Japanese Math Olympiad 0:08:49

Japanese Math Olympiad | A Very Nice Geometry Problem

Q455 | Math 0:02:35

Q455 | Math Olympiad | Geometry | Cyclic Quadrilateral | Ptolemy Theorem | Angle Bisector

Olympiad Geometry Problem 0:11:05

Olympiad Geometry Problem #10: Isosceles Triangle, Midpoints, Perpendiculars

Olympiad Geometry Problem 0:05:57

Olympiad Geometry Problem #56: 30 Degree Angle, Find Length

USNCO 2020 Local 0:25:08

USNCO 2020 Local Exam Problem 49 to 60

Russian Math Olympiad 0:27:41

Russian Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods

Olympiad Geometry Problem 0:13:09

Olympiad Geometry Problem #20: Orthocenter, Angle Bisector, Tangent

BMO2 2019 Q1 0:07:55

BMO2 2019 Q1 - A Nice Geometry Problem

Lay Hand Prayer,Bishop 0:00:27

Lay Hand Prayer,Bishop Amardeep Ministry #bishopamardeepministry

2015 IMO PROBLEM 0:10:55

2015 IMO PROBLEM 4 SOLUTION

Sneha Pareek(topper)checking Jee 0:00:35

Sneha Pareek(topper)checking Jee mains result 2022//score 300/300

Olympiad Geometry Problem 0:16:24

Olympiad Geometry Problem #72: Tangent, Isoceles Triangles, Collinear

Комментарии
Автор

Let AB and CD intersect at T. Angle EPB = angle CPF. Therefore PC and PB are isogonals of angle EPF. By the isogonal theorem PG and PT are also isogonals of angle EPF. It means that angle TPF = angle GPE. More than that EPFT is cyclic. Therefore angle TPF=angle TEF. So, angle GPE = angle TEF = 90 - angle FEP => PG is perpendicular to EF.

rustamnovikov
Автор

Nice theorem, It's new for me. On having the first glance, I thought it's questions of Complete Quadrilaterals.
Very good question and well explained.

omparkash-njzy