filmov
tv
DM-1- Combinatorics - Sum rule and Product rule

Показать описание
This lecture describes how to count sets using some simple rules called sum rule and product rule
DM-1- Combinatorics - Sum rule and Product rule
RULE of SUM and RULE of PRODUCT - DISCRETE MATHEMATICS
Combinatorics - The Product Rule and Sum Rule
10. Sum Rule and Product Rule - Combinatorics - Gate
Combinatorics: sum rule
[Discrete Mathematics] Rule of Sum and Rule of Product Examples
Basics of Computing || Sum rule || Product Rule || Combinatorics || Discrete Mathematics || DMS
COMBINATIONS with REPETITION - DISCRETE MATHEMATICS
Problems on Rule of Sum and Rule of Product
BASICS OF COUNTING | SUM RULE | PRODUCT RULE | EXAMPLE PROBLEMS ON SUM RULE | COMBINATORICS |
DM-9-Combinatorics-Some previous gate questions
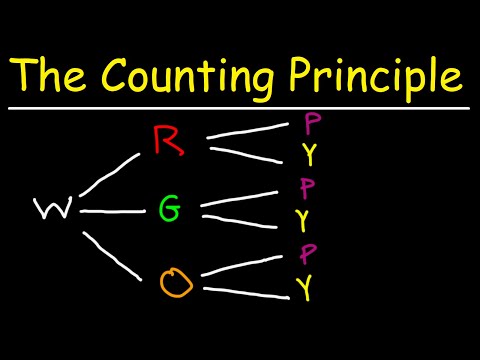
The Fundamental Counting Principle
L15-DM-Basics of Permutation and Combination, Rule of Sum, Rule of Product| SPPU | SE Comp
Counting principles - rule of product & sum || Discrete Structures
DM-8-Combinatorics - Numerical problems related to Combinations
PotW: Combinatorial Sum [Algebra,Combinatorics]
PERMUTATIONS RULE OF SUM
Sum rule principal: counting techniques
[Discrete Mathematics] Rule of Sum and Rule of Product
Basics of Counting
COUNTING|Rule of Sum and Product| BINOMIAL Coefficient and Identities|Permutation and Combination
Rule of Sum and Rule of Product
Product Rule vs Sum Rule
DM-4-Combinatorics- Examples of counting combinations
Комментарии
 0:29:50
0:29:50
 0:09:23
0:09:23
 0:04:11
0:04:11
 0:02:36
0:02:36
 0:10:14
0:10:14
![[Discrete Mathematics] Rule](https://i.ytimg.com/vi/t0us-MXrFZg/hqdefault.jpg) 0:06:00
0:06:00
 0:11:11
0:11:11
 0:13:35
0:13:35
 0:10:33
0:10:33
 0:12:41
0:12:41
 0:18:25
0:18:25
 0:09:06
0:09:06
 0:07:10
0:07:10
 0:10:52
0:10:52
 0:05:42
0:05:42
 0:07:35
0:07:35
 0:03:02
0:03:02
 0:05:35
0:05:35
![[Discrete Mathematics] Rule](https://i.ytimg.com/vi/MmzJF2L_5PA/hqdefault.jpg) 0:11:12
0:11:12
 0:30:52
0:30:52
 0:15:49
0:15:49
 0:02:41
0:02:41
 0:01:12
0:01:12
 0:04:23
0:04:23