Wythoff's Game (Get Home)

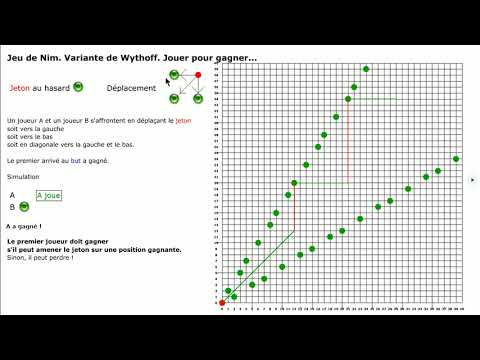
Wythoff's Game is played on a chessboard. Two players take it in turns to move a piece. That piece can move any number of square to the left, and number of squares down, or any number of squares on a down-left diagonal. The winner is the player who moves the piece to the bottom-left square. What are the losing squares?

--

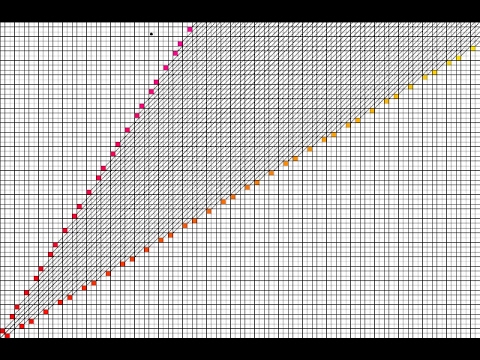
If we call the bottom-left square (0,0) then the losing squares are (1,2), (3,5), (4,7) and their reflections that swap the coordinates.

The losing squares can be generated one at a time using the following two conditions: First, for the nth losing square, the difference between its coordinates is n. And second, each positive integer appears once and only once as either the x or y coordinate of a losing square.

These two conditions have the effect of putting all losing squares on different rows, columns and diagonals.

In 1907, Willem Wythoff proved that the nth losing square has coordinates (n*phi, n*phi^2) where phi is the golden ratio (1.618), and the two coordinates are rounded down to the previous integer. He showed that the golden ratio is the only number that will work in this way, giving the desired two properties of losing squares.

Wythoff's Game on Wikipedia:

[LVo]

Simple: Think of the red and blue piles as the x and y coordinates. You can either subtract from x by going left, subtract from y by going down, or subtract the same amount from both by going down and left

[elliemay]

This happy little man makes maths so interesting and shows me that there is order in this chaotic world of ours.

[pegy]

We've had surprise pi, surprise e, and now surprise Golden Ratio. I'm not sure what you have left, but I'm sure you'll surprise us.

[otakuribo]

⬅️ movement = the blue Nim pile,
⬇️ movement = the red Nim pile,
↙️ movement = equal amounts from both piles

Still, I can't help but be amazed that φ is coming out of this game, rather than something like √2, since it involves diagonal movement. I usually associate φ more with Fibonacci and Fibonacci-like sequences...

[Anonymous-jono]

Golden Ratio is the last thing I'd expect to get in that kind of game...

I guess this means that when playing in a hundred by hundred chessboard, unless one player would actually bother memorizing all of the key squares, the winning chance is equal until... someone can trace the key squares...

[Janiprox]

Your enthusiasm is charming... I have no idea what all that meant, but I loved watching

[TuberTugger]

Anyone curious about his open ending.

Removing from one pile is essentially moving along that axis any number, and taking evenly from both is essentially a diagonal move. So yes, the two games are identical. You just have squares to move instead of counters to take away.

[rasowa]

The most astonishing thing is that this method of generating x and y described at 2:06 will give x/y approaching golden ratio. Wow, didn't expect that!

[OlafDoschke]

In regard of game equivalence, the "two-piles Nim game" simply can be visualized by taking the two piles as x and y coordinates.

Just one note about the symmetry. Though we have the symmetry, we cannot play this game on only half the board (including the middle diagonal, of course). Just think about starting in the third column. If the losing square on c2 or (2, 1) does not exist, the reason all squares above it are winning squares is gone (two can still reach (1, 2), but most of them not). This causes another square of the c column to become a losing square and has a ripple effect, which causes a much simpler pattern sequence of losing squares.

The half-board then would look like this:
𝚆𝚆𝚆𝚆𝚆𝚆𝚆𝚆
𝚆𝚆𝚆𝙻𝚆𝚆𝚆𝚇
𝚆𝚆𝚆𝚆𝚆𝚆𝚇𝚇
𝚆𝚆𝙻𝚆𝚆𝚇𝚇𝚇
𝚆𝚆𝚆𝚆𝚇𝚇𝚇𝚇
𝚆𝙻𝚆𝚇𝚇𝚇𝚇𝚇
𝚆𝚆𝚇𝚇𝚇𝚇𝚇𝚇
𝙻𝚇𝚇𝚇𝚇𝚇𝚇𝚇

Where 𝚇 is unallowed (removed half), 𝙻 is losing and 𝚆 is winning square as used here by others. (By the way: Using MATHEMATICAL MONOSPACE CAPITAL letters helps here to have that monospaced section in an otherwise proportional font)

Losing squares now are all (1, 2) steps from (0, 0), so all (n, 2n) squares are losing squares and this would become rather boring. So the interesting constellation of losing squares only is induced by the lower half of the board.

[BigDaddyWes]

The two colors are equal to the x and y axis with the bottom left corner being zero. All you are doing when you move down or to the left is subtracting from whatever distance you started with. Diagonally you are always subtracting the same number from both x and y. Really cool adaptation of the same game.

[fejfo]

The games are equivalent because 1 pile is an x coordinate and 1 pile a y, (0, 0) is the home. By removing some number from one pile you move towards the home on a row/colum and by removing from both you move diagonally.

[MitkoNikov]

What about a 3D equivalent game? Are the maths going to be the same? Interesting thought.

[mahmoudelsharawy]

They're equivalent because you can start off with a number of red and blue counters, telling you the coordinates of where you are on the chess board. (Origin at bottom left.) Then taking red counters is the equivalent of going left by that number of pieces. Taking blue counters is the equivalent of going down by that many counters. Taking both red and blue counters is going diagonally. It has to be the same amount because you are only going on a perfect bishop-like diagonal.
(Note that red and blue can be switched, and it doesn't effect the game. This is equivalent to the symmetry of the board along the line y=x.)

[TStoneEntertainment]

To equivalence: i would represent all possible states on a 2d grid. Number of one color on the x-axis and number of the other color on the y-axis. This way going left and down is the equivalent of taking from one color and going cross is the equivalent of taking equal amount from both. So we can go down, left and cross-down (as in the original) and our goal is to get to the bottom left square (as in the original). That's a beautiful representation! Would have never thought about this, thanks for sharing.

[danicarovo]

Hey James, I just wanted to tell you that I really appreciate the content that you put up there. I am a senior high-school student and your videos have helped to show me a lot of fun and fascinating sides of math I didn't know before. Seeing your passion makes me love math even more than I did before, so much so that now I'm thinking about taking a math major in university.:)

Math is pure awesome, and the fact that you're showing it and spreading it to the world is neat and much needed.
I guess that's all I wanted to say. Keep up the awesome work!:) ♡

[josip_anton_bilic]

Taking a red disks is like moving to the left, and the blue as moving down, taking both is diagonal, when no more are left youre at the bottom left corner, when theres 7 in both piles youre at top right

[XMegaJuni]

more games. This is great! You are a brilliant teacher

[FlyingOctopus]

Fun fact: if we have two real positive numbers x, y then 1/x+1/y=1 if and only if every positive integer appears in sequence {⎿nx⏌} or {⎿ny⏌} (n is a positive integer). We can replace the 1 with 2(3, 4, ...) and then every integer appears twice (thrice, ..) in a sequences.

[Adowrath]

The equivalence is actually pretty easily proven: The amount of red or blue dots corresponds to your position on the board, 0-indexed. 1 blue and 2 reds is a losing 'square' or 'dot pair', as is 2b1r, etc.
Removing blue dots is equivalent to moving along one axis, i.e. the x-axis, towards zero, the bottom of the board. Same for red and the y-axis. If you remove both, you get the diagonal movement.

[hansmuller]

Each pile is a coordinate, diagonal is 1:1 ration. Oh James, that was too easy ;)