filmov
tv
Proof of the reduction formula for integral of tan^n(x) using the usual trick for powers of tangent.
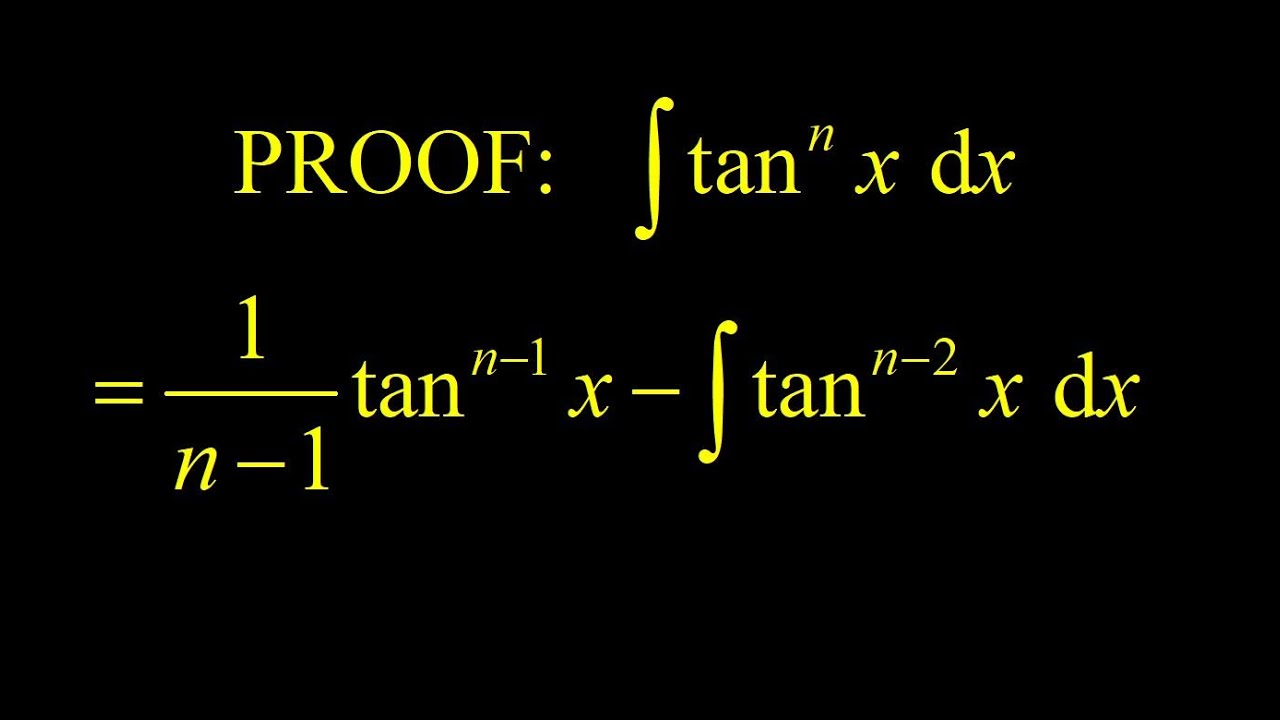
Показать описание
00:00 The integral of tan^n(x) where n is an integer greater than 1 is calculated using the usual trick for powers of tangent. The result is the proof of the reduction formula for tan^n(x).
00:21 Illustrating by example: we start with a simple example of integral tan^4(x). The standard approach here is to split off a factor of tan^2(x), then use the identity tan^2(x)=sec^2(x)-1. After distributing, the result is one term that has a power of tangent next to secant squared, then an additional term with a lower power of tangent. The first term is handled quickly by using the chain rule backwards, because the derivative of the tangent is secant squared. We show that the integral of tan^4(x) follows the power reduction formula after using this approach.
01:59 Apply the standard trick for powers of tangent to the general integral (tan(x))^n: to apply the same trick to the general proof of the reduction formula, we split off a factor of (tan(x))^2 and apply the same pythagorean identity. This gives us two terms, one that is easy to integrate using the chain rule backwards, and the other resulting in an integral of tan^(n-2)(x). After computing the chain rule backwards integral, we obtain the power reduction formula for the integral of tangent to the nth power. QED
00:21 Illustrating by example: we start with a simple example of integral tan^4(x). The standard approach here is to split off a factor of tan^2(x), then use the identity tan^2(x)=sec^2(x)-1. After distributing, the result is one term that has a power of tangent next to secant squared, then an additional term with a lower power of tangent. The first term is handled quickly by using the chain rule backwards, because the derivative of the tangent is secant squared. We show that the integral of tan^4(x) follows the power reduction formula after using this approach.
01:59 Apply the standard trick for powers of tangent to the general integral (tan(x))^n: to apply the same trick to the general proof of the reduction formula, we split off a factor of (tan(x))^2 and apply the same pythagorean identity. This gives us two terms, one that is easy to integrate using the chain rule backwards, and the other resulting in an integral of tan^(n-2)(x). After computing the chain rule backwards integral, we obtain the power reduction formula for the integral of tangent to the nth power. QED
Комментарии
 0:12:26
0:12:26
 0:38:21
0:38:21
 0:07:28
0:07:28
 0:10:24
0:10:24
 0:11:43
0:11:43
 0:09:38
0:09:38
 0:05:59
0:05:59
 0:08:53
0:08:53
 0:16:34
0:16:34
 0:02:49
0:02:49
 0:07:40
0:07:40
 0:05:33
0:05:33
 0:10:15
0:10:15
 0:07:00
0:07:00
 0:01:31
0:01:31
 0:03:18
0:03:18
 0:04:57
0:04:57
 0:07:54
0:07:54
 0:03:32
0:03:32
 0:05:11
0:05:11
 0:05:33
0:05:33
 0:06:14
0:06:14
 0:00:33
0:00:33
 0:02:27
0:02:27