Heapify - build a heap from any arbitrary array. - Java Algorithms Tutorial

Heapify - build a heap from any arbitrary array. is a free tutorial by Shibaji Paul from Java Algorithms course
Link to this course(Special Discount):
This is the best Java Algorithms Course
Course summary:
How to analyse an algorithm, understanding of worst case, best case and average case complexities, How to estimate them using Big O, Big Omega and Big Theta notations.
Seven (7) most important comparison based sorting algorithms, #Bubble Sort, #Selection Sort, #Insertion Sort, #Shell Sort, #Quick Sort, #Merge Sort and #Heap Sort.
Students will get to know details of #heap data structures along with heap operations while leaning heap sort.
They will experience and understand how to execute program on various input sizes and compare the execution time between different input sizes using graph.
English [Auto]
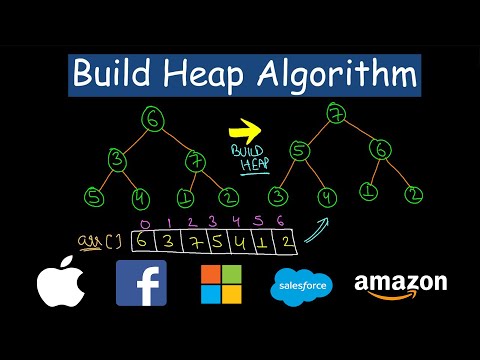
Hello and welcome back in this tutorial and good explain how we can build a maxi from a given in each area that Prosody is popularly known as Hippi fight operation. They can and example at 8 to 9 elements that you can see at the bottom of the screen that they're responding almost complete by really truly present vision is also visible. Now this is an arbitrary area and definitely not a hit. You either do the hit in-place using this hippy PI operation let's see how you can do that. We going to apply the ad just operation that we have understood in the last tutorial for building this operation. Previously a tree with only one node is always a hip. That is we can all of us think a history look at at any leaf isn't it. So you see that ad index 9 which is a leaf we can consider a maxi tree root it at next 9. Same for other lips. Therefore for any almost complete binary tree all leaps can be considered as a Hebrew. We can find leaves up to indexed and divided by two plus one for any almost complete binary tree. As you can see for example it is 9 that Apel number of elements and N divided by two is 4.5. We'll take the flow value. That means four plus one is five. So invite two plus one is five. So all nodes up in five are leaps and they are obviously Hippe trivially. So now from index n divided by two of two index one we can offset that a heap is rooted at B's in this case however for index four. You can see that a heap is maintained at its left child at index 8 and also at X right chimed. That is at index 9 because they are leaps. So we just can make a call to the just operation and just index 4. So that Maxy is maintained at index for earlier when we understood this at just operation. We saw that agist operation at just a particular index. If its left child is a hip and if its right child is a hip then the operation can make that index a hip. So on calling the ad just to make a hit at this for now we have Max hip maintained an index for now the hip operation Dessa starts adjusting the knots so that each of them is a hip starting from index and divided by two up to index one. So his fight executes a loop as it can see starting from equals calls by two and goes up to 1 on each ration it reduces. I'd buy one and all that at just. Operation for index. I'm so four equals four. I just did the hip at index four. Now we did use I'd buy one in the next iteration and Ribault at index three so far equals three. Yeah also the live child is in there 6 and the child is index 7 and they are both a mexi. So we call the ad operation and the industry is adjusted as we reduce it by one in the next iteration and we have I call Still this time. This time again we see that Hape is maintained at an x 4 and 5 that left and the right kind of index 2 respectively. So we call that just for index 2. And it just restores the maxipad index to finally we did use to index one and we see that we have just to keep him safe at index 2 and 3 already. So calling the at just four in this one makes the whole treat grouplet at index 1 as a Maxxie. So this is how the Hippi fire works. OK. Let's not go ahead and find out that worst case complexity of this operation. We can all of us find out a positive integer k such that the total number of elements in the heap and can be expressed in this way in less than it was two to the blockade. Now let me give you an example say that the number of elements in the heap that we have taken what our understanding or perhaps five is nine right. So we can always write nine. Less than equals due to the powerful will always find and EJA something like this for any number and right. So far this nine we have k s for. If you have total number of elements say as 25 then you can write it in this way to 85. That equals two with about 5 right. And that is 32 actually. So for any positive integer. And we can find it and the positive integer k such that we can write. And le