filmov
tv
MIND-BLOWING Radical Math Challenge | Can You Solve This?
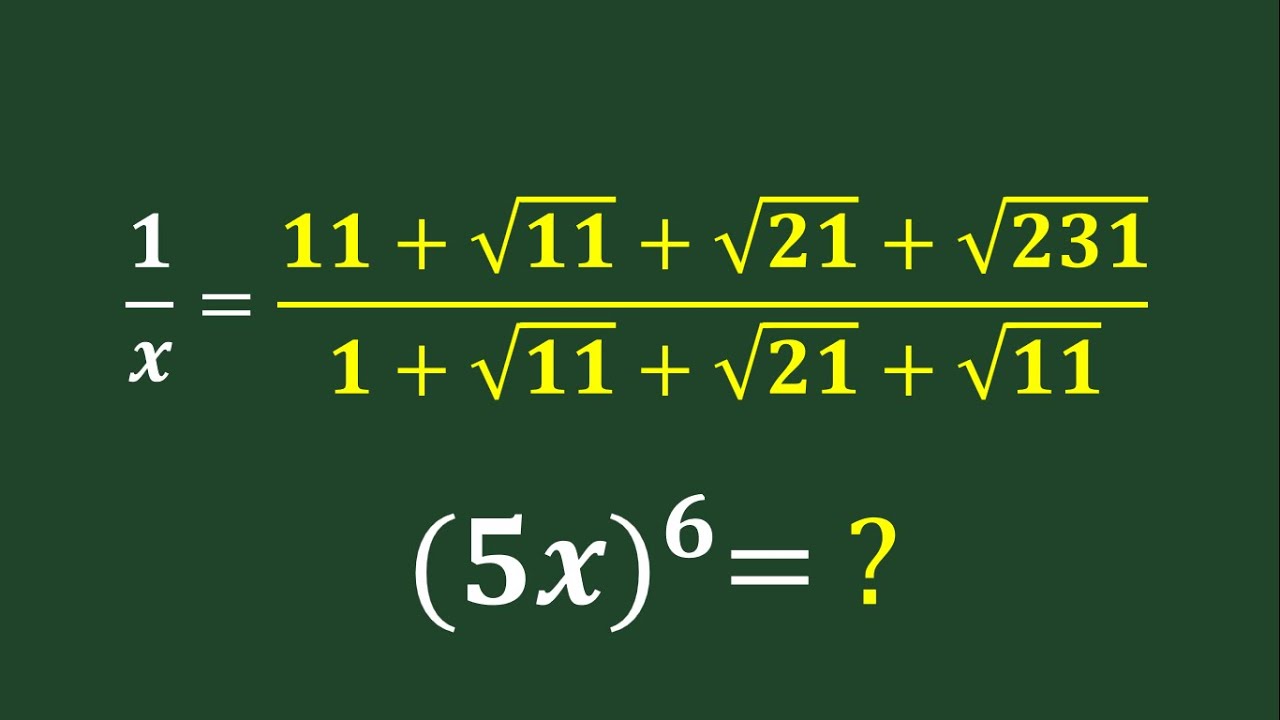
Показать описание
MIND-BLOWING Radical Math Challenge | Can You Solve This?
Welcome to infyGyan!
In this video, we explore an intriguing algebra problem involving radicals, perfect for those preparing for Math Olympiad. This question will enhance the understanding of radical expressions and skills of problem-solving. Watch as we break down the solution step-by-step, providing clear explanations and insights along the way.
If you're a Math Olympiad participant or simply enjoy tackling competitive math problems, this video is for you. Make sure to like, subscribe, and hit the notification bell to stay updated with more exciting math challenges. Let's solve this radical algebra problem together!
🔍 In this video:
Detailed walkthrough of a challenging algebra problem.
Tips and tricks for solving complex radical expression.
Encouragement to enhance your problem-solving skills and mathematical thinking.
📣 Call to Action:
Have a go at the problem yourself before watching the solution!
Share your solutions and approaches in the comments below.
If you enjoyed this challenge, give it a thumbs up and subscribe for more intriguing math problems!
🔗 Useful Links:
#algebra #math #algebratricks #education #problemsolving #mathematics #expression #simplification #radical
Don't forget to like, share, and subscribe for more Math Olympiad content!
Thank You for Watching videos !!
Welcome to infyGyan!
In this video, we explore an intriguing algebra problem involving radicals, perfect for those preparing for Math Olympiad. This question will enhance the understanding of radical expressions and skills of problem-solving. Watch as we break down the solution step-by-step, providing clear explanations and insights along the way.
If you're a Math Olympiad participant or simply enjoy tackling competitive math problems, this video is for you. Make sure to like, subscribe, and hit the notification bell to stay updated with more exciting math challenges. Let's solve this radical algebra problem together!
🔍 In this video:
Detailed walkthrough of a challenging algebra problem.
Tips and tricks for solving complex radical expression.
Encouragement to enhance your problem-solving skills and mathematical thinking.
📣 Call to Action:
Have a go at the problem yourself before watching the solution!
Share your solutions and approaches in the comments below.
If you enjoyed this challenge, give it a thumbs up and subscribe for more intriguing math problems!
🔗 Useful Links:
#algebra #math #algebratricks #education #problemsolving #mathematics #expression #simplification #radical
Don't forget to like, share, and subscribe for more Math Olympiad content!
Thank You for Watching videos !!
Комментарии
 0:14:48
0:14:48
 0:04:02
0:04:02
 0:13:44
0:13:44
 0:10:01
0:10:01
 0:20:42
0:20:42
 0:00:28
0:00:28
 0:03:16
0:03:16
 0:00:37
0:00:37
 5:36:17
5:36:17
 0:11:42
0:11:42
 0:02:21
0:02:21
 0:10:51
0:10:51
 0:00:21
0:00:21
 0:08:02
0:08:02
 0:06:44
0:06:44
 0:00:37
0:00:37
 0:05:06
0:05:06
 0:08:58
0:08:58
 0:21:04
0:21:04
 0:04:38
0:04:38
 0:02:22
0:02:22
 0:11:36
0:11:36
 0:00:17
0:00:17
 0:11:33
0:11:33