What are Autoregressive (AR) Models

preview_player
Показать описание
Time to start talking about some of the most popular models in time series - ARIMA models. First things first, let's look at the AR piece - autoregressive models!
  1. Aric LaBarr
  2. #forecasting
  3. #timeseries
  4. #data science
  5. #data
  6. #autoregressive
Рекомендации по теме
Time Series Talk 0:08:54

Time Series Talk : Autoregressive Model

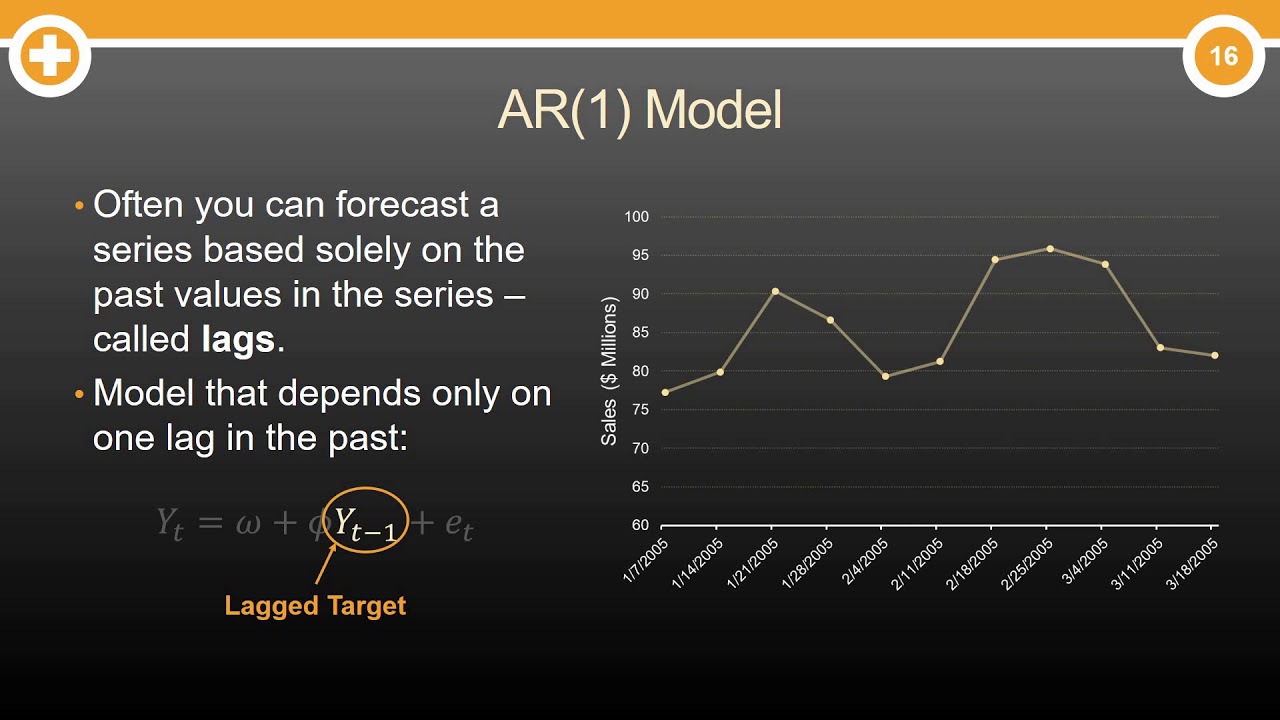
What are Autoregressive 0:05:01

What are Autoregressive (AR) Models

Autoregressive Models | 0:08:47

Autoregressive Models | Auto Regression | Machine Learning for Beginners | Edureka

CFA® Level II 0:08:31

CFA® Level II Quant - Autoregressive (AR) Models: Mean reversion, Covariance Stationarity

Auto Regressive Time 0:10:19

Auto Regressive Time Series Model | AR Model

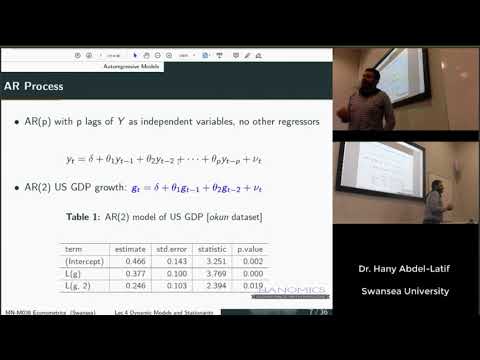
Econometrics - Autoregressive 0:13:43

Econometrics - Autoregressive (AR) Models

Introduction to the 0:03:23

Introduction to the Autoregressive Model

Auto Regression(AR) Model| 0:05:42

Auto Regression(AR) Model| Time Series Forecasting #2

Auto Regressive Models 0:10:20

Auto Regressive Models (AR) | Time Series Analysis | Data Analytics

How to do 0:05:53

How to do Autoregression with Data Analysis toolpak

Introduction to Time 0:10:25

Introduction to Time Series Analysis: AR MA ARIMA Models, Stationarity, and Data Differencing

Auto Regression(AR) Model 0:13:07

Auto Regression(AR) Model in Python| Time Series Forecasting #5|

AR(1) Autoregressive Process: 0:07:50

AR(1) Autoregressive Process: Mean, Autocovariances, ACF

Classical Time Series 0:08:51

Classical Time Series Models AR,MA,ARMA,ARIMA - Understanding time series models in python

Time Series Talk 0:07:12

Time Series Talk : ARMA Model

Autoregressive order 1 0:05:49

Autoregressive order 1 process - conditions for Stationary Covariance and Weak Dependence

What is the 0:05:11

What is the Vector Autoregressive (VAR) Model

Time Series Talk 0:09:26

Time Series Talk : ARIMA Model

What are ARIMA 0:05:07

What are ARIMA Models

LII Concept: Autoregressive 0:02:12

LII Concept: Autoregressive (AR) models

Autoregressive (AR) Time 0:09:24

Autoregressive (AR) Time Series Models

Autoregressive (AR) model: 0:21:49

Autoregressive (AR) model: estimation and stability tests (Excel)

Vector Auto Regression 0:07:38

Vector Auto Regression : Time Series Talk

Autoregressive Models: The 0:15:11

Autoregressive Models: The Yule-Walker Equations

Комментарии
Автор

Thanks Mr. LaBarr, I'm studying for my exam in time series and your videos are very helpful. Greetings from Italy!!!

pettirto
Автор

Came here after being confused by my Lecturer,
Thank you very much for simplifying this!

enock_elk
Автор

Great video. I’ve had a text book about time series that’s been gathering dust because I was afraid of all the symbols. This helps a lot

hugoagudo
Автор

my statistics is very basic and i just needed a forecasting algorithm, this video explained it sooo well

oren
Автор

Thank you, j had seen this equation when a was studying reinforcement learning, it's like the Value function weighted by a discount factor.... Great explanation!!!

williamgomez
Автор

One of the best teachers i’ve ever seen!
Thank you

oq
Автор

just become my lecturer lol. i love the enthusiasm you put in. makes learning more fun lol

clickbaitpolice
Автор

wow your teaching style is really amazing !! please make more videos on time series analysis. we really need your help!!

economicsfriendly
Автор

I like the way you convey the intuition behind AR and MA models. One thing that might be confusing is however the terminology, in particular with regard to short and long memory, which is different in common literature. Therein, AR, MA and ARMA models are considered to be short-memory models, because their autocovariances are summable. Also AR models, whose autocovariance function (ACVF) decays quite quickly towards zero for increasing lags, even though the ACVF values in fact never fully reach zero, has summable autocovariances. In contrast long-memory behavior is indicated by a hyperbolically decaying ACVF, which results in an ACVF whose elements are not summable anymore. A popular example is the fractionally integrated ARMA model, often denoted by either FARIMA or ARFIMA, that can still have ACVF values of notable magnitude for large lags.

arnonym
Автор

God bless you for your efforts to explain!

vadimkorontsevich
Автор

Excellent teaching! Thanks for your good work Aric!

felipedaraujo_
Автор

Hi Dr Aric LaBarr you work is Amazing please continue this again

Under 5 minute concept is great

ahsanshabbir
Автор

Excellent contribution, thank you very much

rossijuan
Автор

simple and beautifully explained! thanks!

josealeman
Автор

man, you are incredible!
Im learning ARIMA like im building legos!

valdompinga
Автор

A lot of overlap here with an infinite impulse response filter from DSP. Im about to watch the moving average model video, but am wondering if that is the finite impulse response equivalent :)

Atrix
Автор

Hi Aric!
This was such a splendidly explained video. I have a doubt though about NARX. Do they function the same way as this one (explained in the video) because NARX is also autoregressive model? If not, could you please explain about NARX as well?

NishaSingh-qfit
Автор

Nice video. Will you be making something about the ARCH/GARCH model :-)

dineafkir
Автор

Can you explain the difference between Static, Dynamic and Autoregressive Probit models?

dipenmodi
Автор

Hi Aric, thanks for the explanatory video. Can it be said that AR(1) is equivalent to Single Exponential Smoothing algorithm because it too depends on the Previous forecast and error.

kumaratuliitd