Phase space & Liouville's Theorem

preview_player
Показать описание
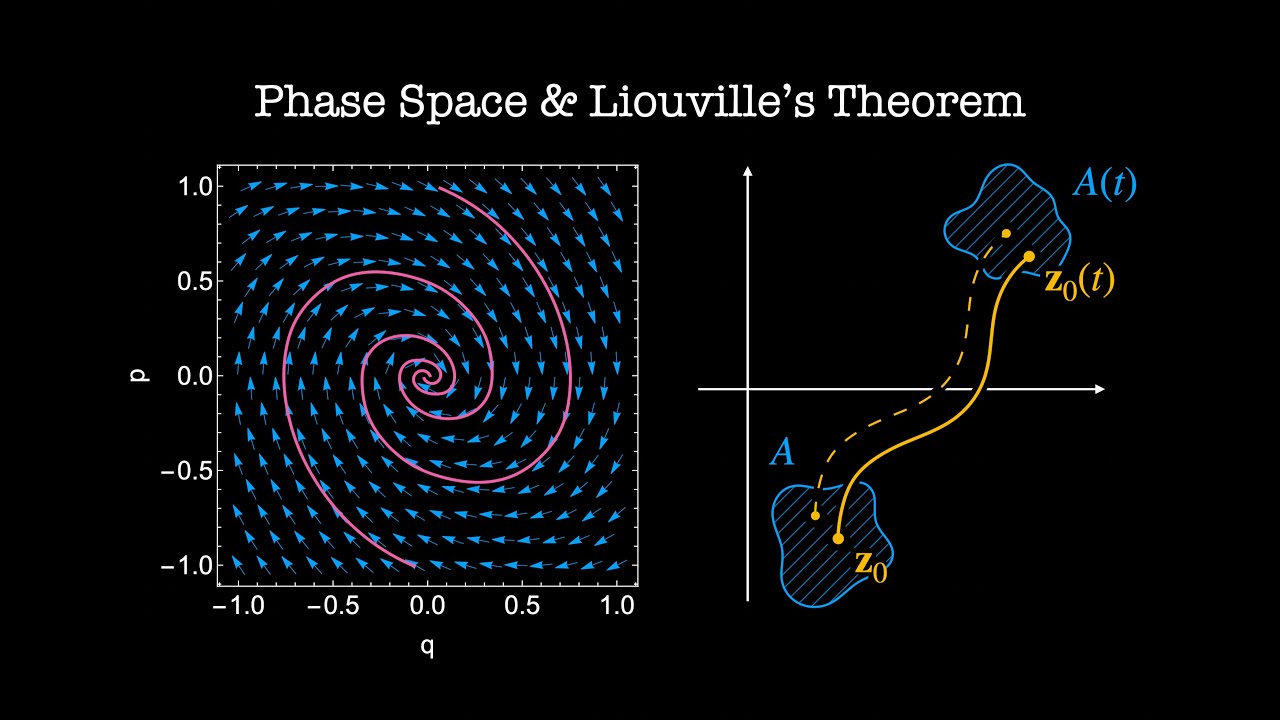
Hamiltonian dynamics exists in phase space -- a space of formed of all the generalized positions and generalized momenta. We explore ways to solve Hamilton's equations in this space.

Music "Everything" by Vi Hart
  1. Sabetta Talks Math
Рекомендации по теме
Phase space & 0:10:59

Phase space & Liouville's Theorem

Liouville and Noether's 0:03:40

Liouville and Noether's theorem | phase space, conservation laws and symetries

Phase space and 0:42:35

Phase space and Liouville's theorem

Classical Mechanics, Lecture 1:20:27

Classical Mechanics, Lecture 19: Hamiltonian Evolution on Phase Space. Liouville's Theorem.

Liouville's theorem 0:31:24

Liouville's theorem

Liouville's Theorem through 0:13:37

Liouville's Theorem through Symplectic Geometry

Mathematical proof of 0:11:13

Mathematical proof of Liouville theorem

liouville s theorem 0:44:32

liouville s theorem |phase space statistical mechanics lecture

Liouville's Theorem and 0:29:10

Liouville's Theorem and phase space

Simple proof of 0:04:35

Simple proof of Liouville's theorem

Liouville's Theorem 0:29:39

Liouville's Theorem

Hamiltonian Mechanics: Liouville's 0:53:51

Hamiltonian Mechanics: Liouville's theorem

Statistical Mechanics 2 1:23:18

Statistical Mechanics 2

Phase Space & 0:10:17

Phase Space & Liouvilli Theorem | Easy Method to Understand | SP

Liouville's Theorem 0:08:35

Liouville's Theorem

PG TRB Physics 0:10:03

PG TRB Physics Statistical Mechanics Phase space, Liouville's theorem

Liouville's Theorem. 0:55:13

Liouville's Theorem.

Let's Learn Physics: 2:28:01

Let's Learn Physics: Chaos in Phase Space

Liouville’s Theorem 0:00:15

Liouville’s Theorem

LIOUVILLE'S THEOREM|| 0:07:44

LIOUVILLE'S THEOREM||

Statistical Mechanics - 0:53:12

Statistical Mechanics - Classical Statistics : Liouville’s Theorem - Classical Version

Liouville's theorem 0:20:06

Liouville's theorem

Statmech3 Ensemble theory 0:48:09

Statmech3 Ensemble theory and Liouvilles theorem

Liouville Theorem | 0:04:12

Liouville Theorem | #7 Analytical Mechanics for Chemistry

Комментарии
Автор

ung phys student here and I got your videos recommended to me from GT, I love the way you present this thank you for the effort you put in these videos.

sdmcal
Автор

One point of critique, you show a phase space plot with spiralling motion. However, Hamiltonian systems never have a sink or source at a singularity. Great video nonetheless!

MGB-wzjz
Автор

so well constructed and so well spoken!! tysm

rishecks
Автор

This channel is a gem for physics students. Subscribed.

takispedaros
Автор

Wonderlful explanation. Very much appreciated!

osmanhussein
Автор

The "proof" given at 6:36 doesn't seem too convincing, at least visually I can imagine a lot of points outside A(t) where the trayectorias do not cross. Besides that, great video and a very good topic

kierkegaard
Автор

Enjoyed this...at (e.g.) 9:10, why do you use cursive delta in the integral? At 8:17 also, dA = Int (n.v dt)dg and all the d's are cursive, like variational notation?

eastofthegreenline