filmov
tv
Imre Barany - Vector-sum Theorems, Their Relatives, and Applications

Показать описание
Imre Barany presents an extended lecture on "Vector-sum Theorems, Their Relatives, and Applications"
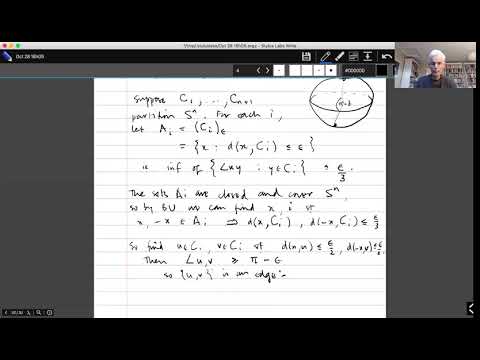
About hundred years ago, answering a question of Riemann, Steinitz proved the following result. Let B be the unit ball of the Euclidean norm in R^d and assume that V is a finite subset of B and the sum of the elements in V is zero. Then there is an ordering v_1,...,v_n of the element of such that all partial sums along this ordering have norm smaller than 2d. I'm going prove this remarkable theorem and explain some of its extensions and generalizations. The result has many applications in various fields of mathematics including for instance in analysis, mathematical programming, scheduling, etc. The lecture covers some of these applications as well.
About hundred years ago, answering a question of Riemann, Steinitz proved the following result. Let B be the unit ball of the Euclidean norm in R^d and assume that V is a finite subset of B and the sum of the elements in V is zero. Then there is an ordering v_1,...,v_n of the element of such that all partial sums along this ordering have norm smaller than 2d. I'm going prove this remarkable theorem and explain some of its extensions and generalizations. The result has many applications in various fields of mathematics including for instance in analysis, mathematical programming, scheduling, etc. The lecture covers some of these applications as well.
 2:35:38
2:35:38
 0:57:54
0:57:54
 1:04:45
1:04:45
 1:01:22
1:01:22
 0:36:00
0:36:00
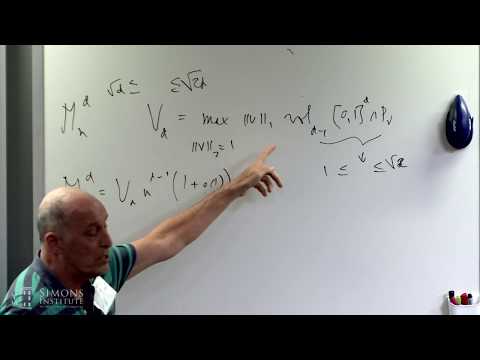 0:29:42
0:29:42
 0:42:23
0:42:23
 0:58:01
0:58:01
 0:52:54
0:52:54
 0:39:43
0:39:43
 1:00:18
1:00:18
 0:51:01
0:51:01
 0:29:22
0:29:22
 1:17:29
1:17:29
 0:42:14
0:42:14
 1:05:59
1:05:59
 0:59:06
0:59:06
 1:03:00
1:03:00
 0:44:39
0:44:39
 0:59:51
0:59:51
 0:14:58
0:14:58
 1:06:02
1:06:02
 0:51:15
0:51:15
 0:50:38
0:50:38