Understanding Gradient Descent for Machine Learning with an Example || Lesson 9 || Machine Learning

#machinelearning#learningmonkey

In this class, we will have an understanding gradient descent for machine learning with an example.

This is a computational method for finding the minimum point on a function.

At what value of x we have minimum y.

The situation at which this method is useful is discussed in the previous discussion.

Let's take an example and understand how gradient descent works.

Take function y=(x-1)^2 +1.

Before going to concept lets refresh some of the concepts.

Derivative gives the slope of a function at a given point.

Slope means a change in y /change in x.

The slope is +ve if the increase in x at a given point y also increase

The slope is -ve if the increase in x at a given point y decrease

To identify the minimum point.

Randomly select an x value. Here we are selecting x=5

Derivative of the function is dy/dx=2x-2.

substitute 5 in the derivative equation ie 2*5 -2 =8.

so slope at x =5  is 8

+ve slope means x increase y increase.

Understand we have to identify the minimum y value. Ie reduce x value.

Lets take x= -5.

At x=-5 slope = 2*-5 -2 = -12.

The slope is -ve means x increase y decrease.

Y moving towards minimum. So increase x.

To meet the above conditions gradient descent uses the equation xnew = xold - alpha*[dy/dx] xold.

Check the above equation if the slope is +ve we subtracting from xold value ie decreasing x value.

If the slope is -ve than -ve * -ve we get +ve means we are adding value to xold. Increasing x value.

The above equation always push x value to the minimum y value.

Assume alpha = 0.2. we will understand why we use alpha at the end of the discussion.

We understand this wit an example

let's take x=5

so xold =5

find xnew value

xnew = xold – alpha*[dy/dx]xold  here xold = 5 dy/dx = 2x-2.

xnew = 5 – 0.2 * [2*5-2].

xnew = 5 – 0.2 * 8.

xnew = 5 – 1.6.

xnew = 3.4.

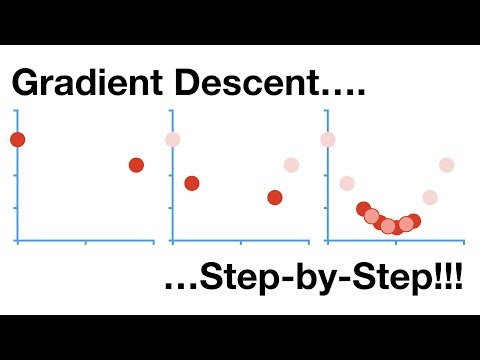
Observe from the above figure x moving to minimum y point.

Now xold = 3.4

again find xnew

xnew = xold – alpha [dy/dx]3.4

xnew = 3.4 – 0.2 * [(2 * 3.4) – 2]

xnew = 3.4 – 0.2 * 4.8

xnew = 3.4 – 0.96

snew = 2.44

again x moving near to minimum y value.

So keep repeating this computation till xnew value reaches minimum y value.

How we know x reaches to minimum y value.

Observe from the above figure when x reaches to point p1. When we find the xnew value at p1.

Xnew moves to p2 point. P2 is on the other side.

At p2 slope is -ve. So when we find xnew again at p2 we increase x value and move to p1 side again.

This we call it convergence. Ie x moved to minimum y. we can stop computing.

Let's understand what's the use of alpha.

Lets take alpha = 0.4.

xnew = xold – alpha*[dy/dx]xold  here xold = 5 dy/dx = 2x-2.

xnew = 5 – 0.4 * [2*5-2].

xnew = 5 – 0.4 * 8.

xnew = 5 – 3.2.

xnew = 1.8.

Observe as the alpha value increased fro 0.2 to 0.4.

x value takes a long jump.

At alpha = .2 x jumped from 5 to 3.4.

at alpha = .4 x jumped from 5 to 1.8.

as alpha value increases x takes long jump ie x moves to minimum point very fast.

Convergence is fast with a big alpha.

But with large alpha, the problem is we can not have a better approximation.

Why not better approximation?

Observe from the above figure.

The point in red color. From there, its taking long jump means its moving to the other side.

Observe the x value swaps on both sides. And it's far from the actual minimum.

That's the reason large alpha doesn't have better approximations.

If needed better approximation use small alpha.

if needed fast convergence use large alpha.

This understanding of gradient descent will help a lot in Machine learning.

[CSD-]

Hatsofff to your explanation..I think no one make this much clear to a begginner so nice of i sir..

[pratheebac]

Crystal Clear explanation, really applauding efforts.

[srikanth]

U did more struggle to make us understand this concept. Thank you 😀

[hasanmahmud]

finally understand the concepts clearly, lots of thanks.

[devinenitejaswini]

Another main advantage of lower alpha is that, it converges to global minima rather than converging to local minima which is important regarding convergence of an algorithm in machine learning algorithms

[srikanth]

Finally here gradient means, required range or selectable change in y.

[Rohit-bygl]

From where we got this equation X new = x old - Alpha * dy/dx ?

[tusharsalunkhe]

If we have a non convex function then it will have local minimum and global minimum, so how will we come to know that by using Gradient Descent method the minimum point we have got is local / global minimum? or Gradient Descent method is used for convex function only ?

[anupprasad]

Sir, one doubt... How to select the value of alpha or it is selected by the machine...

[himanshumangoli]

we are doing gradient descent to find the minimum point where our slope is near about to zero

[raghavendragoud]

Can we call alpha as a momentum term that helps to convergence fast ? Then why we use learning rate ?

[srikanth]

Can you able to write formula for y new from y old by taking gardiant and x values

[malothnaveen]

hi, that formula is fine how do u know the shape of gradient descent is convex

[srikanth]

X new = x old - gradient * slope. From this formula, if we are in -ve val of x, the x new will be increasing, in above example, u took x value as positive so xnew value decreases. Am I correct.

[manivannanparthasarathi]

The graph is wrong for your slope (x=-5, the value is -12). When you take derivate for the equation then the equation becomes linear. Then how can we represent the graph. Can you please explain

[sushilvijayvargiya]

At this point I don't understood how you compute the equation x(new)=x(old)- alpha* slope at x(old)?

[aasifKhan-rdwl]

nice explanation. One question, as you showed us in previous video that we can equate the derivative function to zero, who we do use this complex and lengthy process to find (or approximate) the minimum value. cant we directly equate it to zero and find min value?

what are the advantages/disadvantages of GD compared to a direct calculation.