filmov
tv
Método de la Bisección | | UPV
Показать описание
Título: Método de la Bisección
Descripción automática: En este video, la profesora del Departamento de Matemática Aplicada introduce el método de la bisección, utilizado para calcular de manera aproximada las raíces de ecuaciones que no se pueden despejar algebraicamente. Explica que el método es necesario cuando las soluciones no pueden obtenerse directamente, como en el caso de ciertas ecuaciones profesionales o académicas.
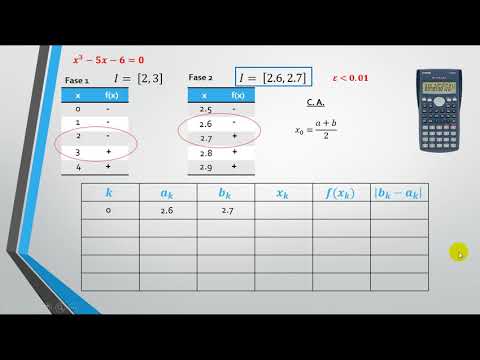
La técnica se basa en el teorema de Bolzano, que parte de la suposición de que la raíz buscada está aislada y es única dentro de un intervalo dado donde la función es continua. El proceso implica dividir repetidamente el intervalo a la mitad y seleccionar el subintervalo que contiene la raíz, según el cambio de signo de la función. Este procedimiento se repite iterativamente, mejorando progresivamente la aproximación de la raíz.
Se destacan las características del método: su convergencia segura hacia la raíz a medida que se aumentan las iteraciones y el establecimiento de criterios de parada basados en el número de iteraciones o una cota de error predefinida. El principal inconveniente es su lentitud en comparación con otros métodos numéricos.
Finalmente, la profesora ilustra el proceso con una ecuación específica, haciendo solo tres iteraciones y animando a los espectadores a participar en el análisis. Concluye la presentación esperando haber aclarado cómo funciona el método de bisección.
Autor/a: Trujillo Guillen Macarena
#Raíces ecuaciones #Método bisección #Cálculo numérico #MATEMATICA APLICADA
Descripción automática: En este video, la profesora del Departamento de Matemática Aplicada introduce el método de la bisección, utilizado para calcular de manera aproximada las raíces de ecuaciones que no se pueden despejar algebraicamente. Explica que el método es necesario cuando las soluciones no pueden obtenerse directamente, como en el caso de ciertas ecuaciones profesionales o académicas.
La técnica se basa en el teorema de Bolzano, que parte de la suposición de que la raíz buscada está aislada y es única dentro de un intervalo dado donde la función es continua. El proceso implica dividir repetidamente el intervalo a la mitad y seleccionar el subintervalo que contiene la raíz, según el cambio de signo de la función. Este procedimiento se repite iterativamente, mejorando progresivamente la aproximación de la raíz.
Se destacan las características del método: su convergencia segura hacia la raíz a medida que se aumentan las iteraciones y el establecimiento de criterios de parada basados en el número de iteraciones o una cota de error predefinida. El principal inconveniente es su lentitud en comparación con otros métodos numéricos.
Finalmente, la profesora ilustra el proceso con una ecuación específica, haciendo solo tres iteraciones y animando a los espectadores a participar en el análisis. Concluye la presentación esperando haber aclarado cómo funciona el método de bisección.
Autor/a: Trujillo Guillen Macarena
#Raíces ecuaciones #Método bisección #Cálculo numérico #MATEMATICA APLICADA
0:08:10
Método de la Bisección | | UPV
0:09:17
Tutorial Metodo de Biseccion
0:10:02
Método de Bisección - Métodos Numéricos
0:33:09
Método de Bisección
0:15:20
Métodos Numéricos: Método de BISECCIÓN, y colocación e interpretación gráfica.
0:15:55
Método de Bisección usando excel, ejemplo 1
0:10:43
Metodo de biseccion
0:11:26
Método de bisección para encontrar raíces (Muy básico)
0:10:29
RE02: Ejemplo del método de bisección
0:14:03
Método de bisección
0:15:55
Metodo de la Bisección
0:10:14
Solucíon de ecuaciones NO lineales (Método de Bisección)
0:07:09
Método de biseccion, metodo de bisección, métodos numéricos, primera parte, parte 1
0:16:04
Métodos Numéricos: Método de BISECCIÓN, EJEMPLO paso a paso.
0:09:52
TEOREMA de BOLZANO, Demostración en solo 10 minutos, Método de la bisección
0:46:13
01 - Métodos numéricos - Método de la Bisección
0:14:37
Método de Bisección en Excel
0:18:15
Método de Bisección - Ejercicio 1
0:35:09
Método de la Bisección ejemplo 1
0:16:38
MÉTODO DE LA BISECCIÓN | MATLAB | PYTHON | MÉTODOS NUMÉRICOS
0:03:47
Método de bisección
0:08:40
MÉTODO DE BISECCION O INTERVALO MEDIO FORMA GRAFICA
0:12:55
Método de Bisección en Matlab
0:14:05
¡SUSCRÍBETE! Métodos numéricos - Método de BISECCIÓN - error estimado - CHAPRA solucionario
Комментарии