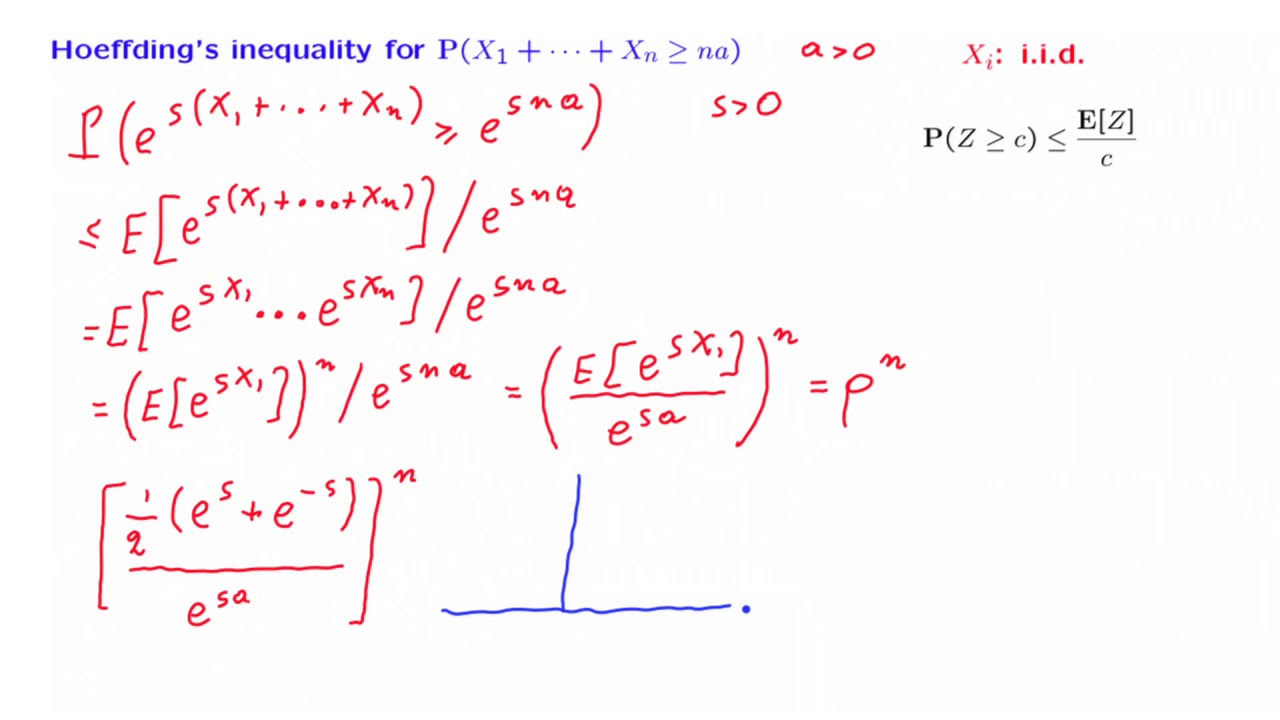
S18.3 Hoeffding's Inequality

MIT RES.6-012 Introduction to Probability, Spring 2018
Instructor: John Tsitsiklis

License: Creative Commons BY-NC-SA

[randomvideos]

Leave it to MIT for the best explanations...

[RealMcDudu]

In case anyone wonders - why there are a lot of different hoeffdings inequalities - I think it depends on the bound of Xi.
Theorem 1 of Hoeffding (and Wassily) paper states that for 0 < Xi < 1 - then E[Xn - E[x] > eps] <= exp{-2nt^2}. The reason we get the result here is with -0.5 instead of -2, is because of the specific case discussed in this video, which is Xi = 1 or -1, with probability of 0.5 for each - in this case the interval of Xi is 1 - (-1) = 2. so we need to use theorem 2 of Hoeffding Wassily, which is for bounded random variables, E[Xn - E[x] > eps] <= exp{(-2nt^2)/((b-a)^2)} - in this case b-a = 2, so the denominator is 4, and so we get that the -2 becomes -0.5. But this is again, just the usage of the general hoeffding theorem for the special case of Xi = 1 or -1 discussed in the video.

[Adityarm.]

This was an amazing expalantion, with all the links touched to the right depth. Thank you!

[mcab]

How come he just announced Y as a standard normal by just dividing sqrt of n at 1:30? Isn't it (Y-nmü)/sqrt(n)sigma by C.L.T? And also what he says after for 2 mins are somewhat ambigious.. Why order of squrt(n) is more likely to occur?

[nagnusyo]

It was proved under the assumption that when RV has zero mean and P(x = 1) = P(x = -1).
I am wondering if this inequality can still hold for RVs that have non-zero mean and non symmetrically distributed.

[HungDuong-dtlg]

At 13:08, where does mu * n come from? What is mu?

[orjihvy]

Are we implicitly assuming standard normal via CLT?

[shakesbeer]

Having Xi IID Bernoulli(p=1/2) seems a bit too restrictive.