filmov
tv
MATRIZ JACOBIANA #01
Показать описание
MATRIZ JACOBIANA #01
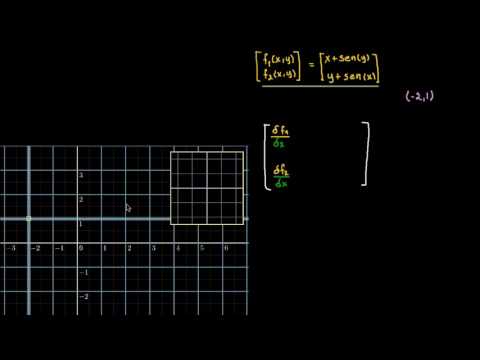
A Matriz Jacobiana é a matriz formada pelas derivadas parciais de primeira ordem de uma função vetorial. Se uma função é diferençável num ponto, a sua derivada é dada em coordenadas pela Jacobiana, mas uma função não precisa ser diferençável para a existência da Jacobiana; basta que as derivadas parciais existam
Derivadas - Matriz Jacobiana
Derivadas Parciais - Diferencial - Matriz Jacobiana
matriz jacobiana para que serve,
matriz hessiana,
exercícios de matriz jacobiana,
determinante da matriz jacobiana,
matriz jacobiana função composta,
matriz jacobiana exercícios resolvidos,
determinante jacobiano definição,
jacobiano exercícios resolvidos
Seja membro deste canal e ganhe benefícios:
Agora no canal Matemática Rapidola, você poderá tornar-se membro do canal nos times de Estatística Básica e Estatística Aplicada.
A Matriz Jacobiana é a matriz formada pelas derivadas parciais de primeira ordem de uma função vetorial. Se uma função é diferençável num ponto, a sua derivada é dada em coordenadas pela Jacobiana, mas uma função não precisa ser diferençável para a existência da Jacobiana; basta que as derivadas parciais existam
Derivadas - Matriz Jacobiana
Derivadas Parciais - Diferencial - Matriz Jacobiana
matriz jacobiana para que serve,
matriz hessiana,
exercícios de matriz jacobiana,
determinante da matriz jacobiana,
matriz jacobiana função composta,
matriz jacobiana exercícios resolvidos,
determinante jacobiano definição,
jacobiano exercícios resolvidos
Seja membro deste canal e ganhe benefícios:
Agora no canal Matemática Rapidola, você poderá tornar-se membro do canal nos times de Estatística Básica e Estatística Aplicada.
0:15:20
MATRIZ JACOBIANA #01
0:00:31
Matriz jacobiana de un campo vectorial #maths #algebra #calculo #matrices
0:09:08
Derivadas - Matriz Jacobiana
0:00:58
LA MATRIZ JACOBIANA
0:03:31
Calculando uma matriz jacobiana
0:02:20
Ejemplo Matriz Jacobiana
0:08:49
Cálculo Avançado - Matriz Jacobiana
0:06:53
A matriz jacobiana
0:05:46
Matriz Jacobiana o Jacobiano
0:05:12
Calculando la matriz jacobiana | Cálculo multivariable | Khan Academy en Español
0:04:35
Matriz Jacobiana
0:06:02
A matriz jacobiana
0:13:34
QUE ES UNA MATRIZ JACOBIANA?🤔 | 👉Como calcularla? | Ejercicio #1
0:10:01
XX. Matriz Jacobiana - Ejemplo 1 (pt1)
0:00:59
🟣EL PODER DE LOS JACOBIANOS🟣 #mateciencias
0:28:53
Aula 6 - Matriz Jacobiana e Sistemas de coordenadas - coordenadas polares, cilíndricas e esféricas....
0:07:54
MATRIZ JACOBIANA Y GRADIENTE DE UNA FUNCIÓN | CÁLCULO MULTIVARIABLE | MR PLANCK
0:08:38
MATRIZ #JACOBIANA GEOMÉTRICA EN #PYTHON | zDynamics
0:13:44
Diferencial, matriz jacobiana y derivadas parciales de una función de varias variables
0:08:34
La matriz jacobiana | Cálculo multivariable | Khan Academy en Español
0:13:29
MATRIZ JACOBIANA #02
0:06:35
MATES. Universidad. Matriz JACOBIANA.
0:06:19
TI 89 MATRIZ JACOBIANA
0:13:23
#DERIVADA DE UNA #MATRIZ #JACOBIANA GEOMÉTRICA | zDynamics
Комментарии