filmov
tv
Tangents to a circle from a point P

Показать описание
Learn how to draw the tangent lines to a given circumference passing through an external given point P.
This YouTube channel is dedicated to teaching people how to improve their technical drawing skills. It focusses on drawing figures from the geometric plane to descriptive geometry and also different systems of technical drawing representation.
If you subscribe, click, like or leave a comment you will be helping us to grow our channel and help more people with their technical drawing skills.
Thank you in advance.
Dubbed by Frank Shaw.
#StayHome and draw #WithMe #Geometry #HowtoDraw
This YouTube channel is dedicated to teaching people how to improve their technical drawing skills. It focusses on drawing figures from the geometric plane to descriptive geometry and also different systems of technical drawing representation.
If you subscribe, click, like or leave a comment you will be helping us to grow our channel and help more people with their technical drawing skills.
Thank you in advance.
Dubbed by Frank Shaw.
#StayHome and draw #WithMe #Geometry #HowtoDraw
TANGENT LINES AND CIRCLES EXPLAINED!
Equation of a Tangent to a Circle - Corbettmaths
Tangents of Circles (1 of 4: What are they?)
Equations of Tangents to Circles (Complete Grade 9 Lesson) | Grade 9 Playlist | GCSE Maths Tutor
Tangents to a circle from a point P
Tangents to a Circle (GMAT/GRE/CAT/Bank PO/SSC CGL) | Don't Memorise
Everything About Circle Theorems - In 3 minutes!
Find Equation of Tangent To Circle Q8 GCSE
How to draw a tangent at a point on the circle
Given a line tangent to a circle find the value of x
How to draw the external tangents to two unequal circles
Tangents from an external point to a circle | construction of tangents to a circle
Writing an equation of circle tangent to the x axis given the center
CIRCLES, CHORDS TANGENTS AND ANGLES. FORM 3 MATHEMATICS
How to Construct Tangents to a Circle From a Point outside the Circle. Tangents to a Circle class 10
Tangents Meeting @ a Point Outside the Circle l How to Find Missing Angles(CIRCLE THEOREMS)
Circles, Angle Measures, Arcs, Central & Inscribed Angles, Tangents, Secants & Chords - Geom...
Construction #9 - Tangent to a Circle From a Point Outside the Circle
JC Graphics - Tangent to a Circle Problems
Equation of a Tangent to a Circle 2 - Corbettmaths
tangents to cirlces with given point outside the circle
Equation of Circle from Tangent [Exam Question]
Construction of tangents to a circle from a point outside a circle | Math | Letstute
Power Theorems - Chords, Secants & Tangents - Circle Theorems - Geometry
Комментарии
 0:05:30
0:05:30
 0:05:03
0:05:03
 0:08:40
0:08:40
 0:52:27
0:52:27
 0:03:51
0:03:51
 0:04:48
0:04:48
 0:04:11
0:04:11
 0:05:41
0:05:41
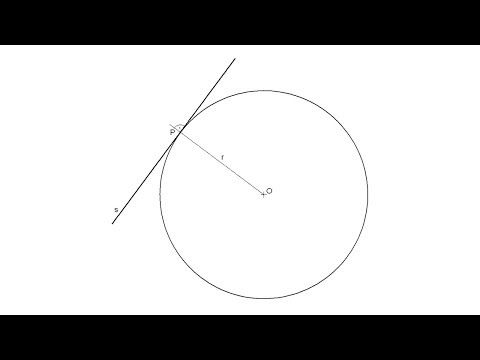 0:01:49
0:01:49
 0:02:09
0:02:09
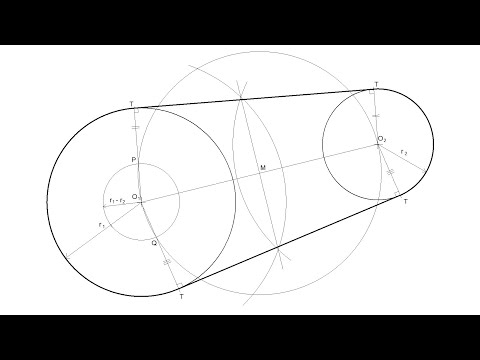 0:04:00
0:04:00
 0:01:12
0:01:12
 0:01:29
0:01:29
 0:09:13
0:09:13
 0:01:41
0:01:41
 0:05:20
0:05:20
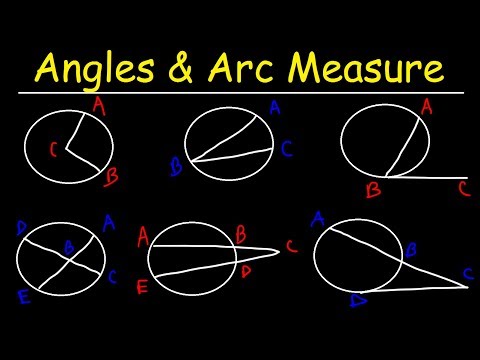 0:32:31
0:32:31
 0:05:39
0:05:39
 0:07:55
0:07:55
 0:03:59
0:03:59
 0:18:36
0:18:36
 0:13:09
0:13:09
 0:09:59
0:09:59
 0:23:01
0:23:01