filmov
tv
Olympiad Geometry Problem #61: Angle Bisector, Perpendicular Bisector Cyclic Quad
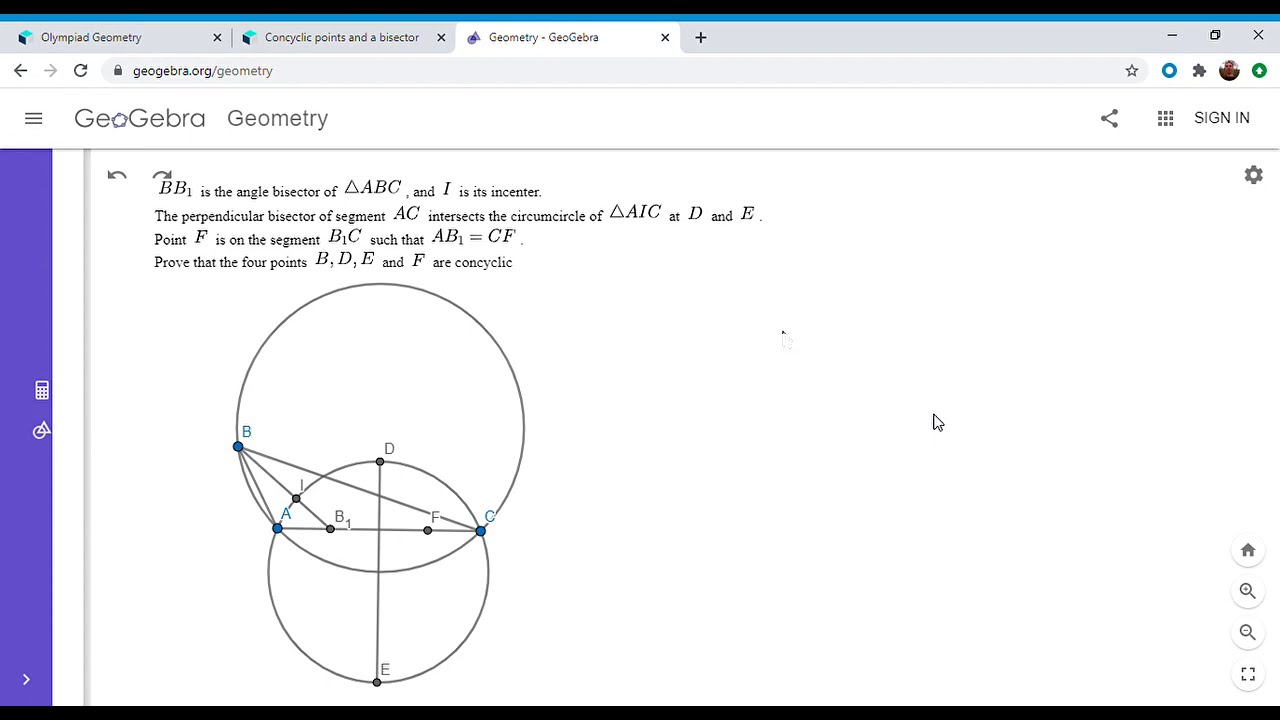
Показать описание
Here is a delightful problem from the Saint Petersburg Math Olympiad this very year in 2020! My inspiration for the solution came from another video on my channel. Enjoy! Link below.
Olympiad Geometry Problem #61: Angle Bisector, Perpendicular Bisector Cyclic Quad
61) Impossible . . . find 'X' #maths #geometry #olympiad
Olympiad Geometry Problem #63: Incenter, Diameter, Equal Angles
Olympiad Geometry Problem #62: Parallel, Tangents, Cyclic Quad
Olympiad Geometry Problem #83: Tangency, Circumcircle, Bisection
Geometry olympiad problem in under 1 min
China Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Topper Vs Back bencher | Exterior Angle Property #shorts #youtubeshorts #ashortaday #viralmaths #fun
USA | Tricky Geometry Olympiad Problem
Hungary Math Olympiad Problem | Best Math Olympiad Problems | Geometry Problem
The Hardest Math Test
Geometry Puzzle: Can You Find the Perimeter of This Triangle
Interesting Figure Question | Math Olympiad
Al-Khorezmi International Mathematical Olympiad | Olympiad problem in 30 seconds #shorts #geometry
LIVESTREAM GEO #61B: We Saw the Second Problem Before, but Still Couldn't Solve It!
Indian mathematical Olympiad Question | RMO Question | Can you solve this Olympiad Question #rmo
NEWYES Calculator VS Casio calculator
simple math
#Geometry Olympiad question #short #Short solution
WHY I HATE MATH 😭 #Shorts
Find the area of triangle ABC | A Nice Geometry Problem | 2 Different Methods to Solve
Solving Geometry Problem For Parallelograms
How to Answer Any Question on a Test
Maths Ki Problem 😜 PIHOOZZ
Комментарии
 0:10:50
0:10:50
 0:01:00
0:01:00
 0:11:55
0:11:55
 0:11:39
0:11:39
 0:12:32
0:12:32
 0:00:55
0:00:55
 0:18:02
0:18:02
 0:00:13
0:00:13
 0:04:59
0:04:59
 0:16:32
0:16:32
 0:00:28
0:00:28
 0:03:28
0:03:28
 0:03:33
0:03:33
 0:01:00
0:01:00
 1:29:02
1:29:02
 0:07:00
0:07:00
 0:00:14
0:00:14
 0:00:12
0:00:12
 0:00:11
0:00:11
 0:00:24
0:00:24
 0:16:31
0:16:31
 0:06:05
0:06:05
 0:00:27
0:00:27
 0:00:23
0:00:23