filmov
tv
The Coxeter Classification 1/2: Combinatorics is hard
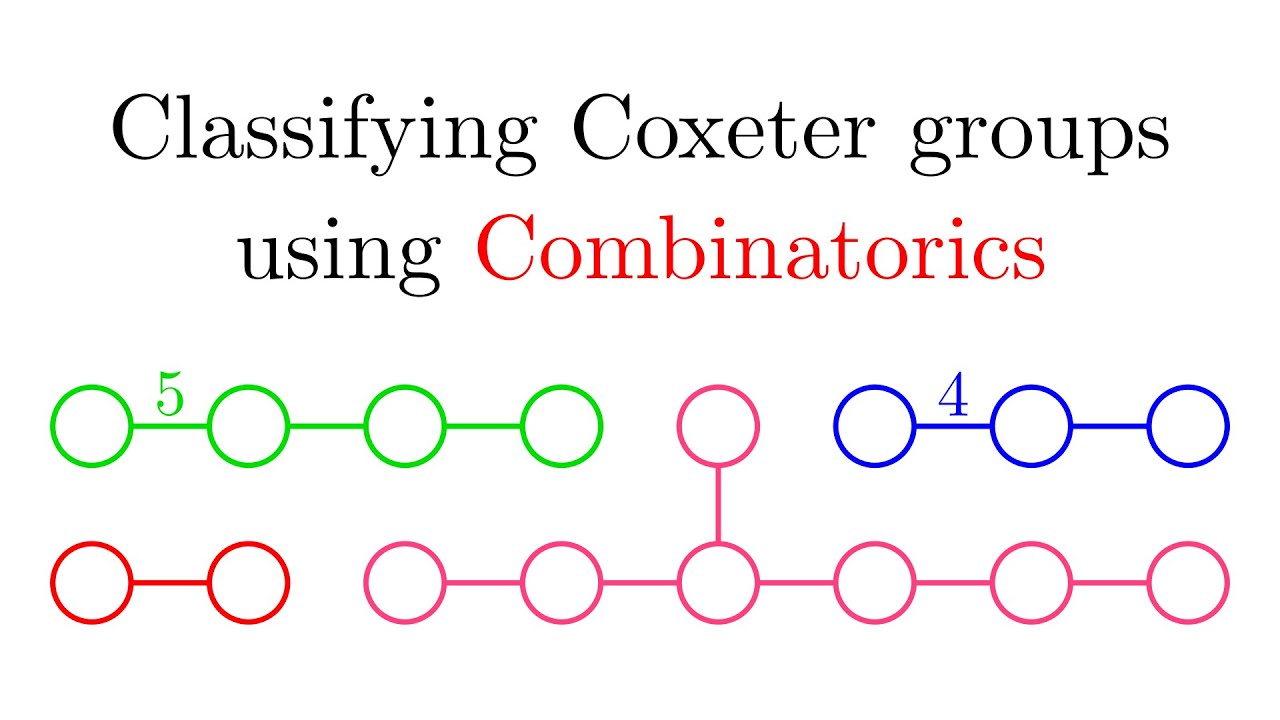
Показать описание
A very hands-on approach to Coxeter systems.
#SoME3
00:00 Opening
02:23 Part 1: Introducing Coxeter systems
10:14 Part 2: Proving things are infinite
15:23 Part 3: Symmetry groups of polyhedra
25:00 Part 4: The exceptional systems
32:18 Conclusion
Some casual overviews of finite groups, if you want a primer for this video:
If you're looking for more detailed proofs of results like the Word Property, I recommend the textbook Combinatorics of Coxeter Groups by Björner and Brenti which covers these in the first 3 chapters.
Small corrections thanks to commentors:
*The word 'prism' at 19:16 should be 'pyramid', or equivalently an asymmetric prism so that reflecting through the length is not a symmetry.
#SoME3
00:00 Opening
02:23 Part 1: Introducing Coxeter systems
10:14 Part 2: Proving things are infinite
15:23 Part 3: Symmetry groups of polyhedra
25:00 Part 4: The exceptional systems
32:18 Conclusion
Some casual overviews of finite groups, if you want a primer for this video:
If you're looking for more detailed proofs of results like the Word Property, I recommend the textbook Combinatorics of Coxeter Groups by Björner and Brenti which covers these in the first 3 chapters.
Small corrections thanks to commentors:
*The word 'prism' at 19:16 should be 'pyramid', or equivalently an asymmetric prism so that reflecting through the length is not a symmetry.
The Coxeter Classification 1/2: Combinatorics is hard
The Coxeter Classification 2/2: Who cares about Representation Theory?
596.1.2 'Braid-a-Grams' and the Coxeter Presentation
What are...Coxeter complexes?
Reflection Groups and Coxeter Geometries
Seminar Soergel bimodules 1 - Coxeter groups, the beginnings
What is...a Coxeter group?
Introduction to Coxeter Groups
Geometric graph theory: Weyl Groups, Root Systems and Quadratic Forms
Escher and Coxeter - a Mathematical Conversation - Professor Sarah Hart
Jodi McWhirter - Ehrhart Quasipolynomials of Coxeter Permutahedra
Geometry Revisted by Coxeter and Greitzer #mathsolympiad #book
Exceptional structures in mathematics and physics from dynamics on graphs
This Week's Finds 5: Coxeter and Dynkin diagrams
Hankyung Ko: A singular Coxeter presentation
Yang Shi: Normalizer theory of Coxeter groups and discrete integrable systems
Coxeter element
Harold Scott MacDonald Coxeter
Coxeter combinatorics and Braid Varieties, Nathan Williams, 16/03/2023
The Most Powerful Diagram in Mathematics
Modern Topology - Lecture 16 - Combinatorial Group Theory
An ICERM Public Lecture: Mirror Mirror on the Wall
Andrea Švob, Minicourse: Construction of combinatorial structures from finite groups. Lecture 1.
Jeroen Schillewaert: Constructing highly regular expanders from hyperbolic Coxeter groups
Комментарии
 0:36:07
0:36:07
 0:41:35
0:41:35
 0:22:25
0:22:25
 0:16:06
0:16:06
 0:08:04
0:08:04
 1:43:56
1:43:56
 0:29:41
0:29:41
 0:44:33
0:44:33
 0:50:20
0:50:20
 0:53:25
0:53:25
 0:22:11
0:22:11
 0:00:58
0:00:58
 0:34:52
0:34:52
 0:59:10
0:59:10
 1:15:38
1:15:38
 0:42:20
0:42:20
 0:05:51
0:05:51
 0:01:58
0:01:58
 0:48:39
0:48:39
 0:45:49
0:45:49
 1:35:04
1:35:04
 1:03:21
1:03:21
 1:22:50
1:22:50
 0:44:41
0:44:41