filmov
tv
A-Level Further Maths H2-04 Hyperbolic Calculus: Non-Stationary Point of Inflection Example
Показать описание
0:06:26
A-Level Further Maths H2-04 Hyperbolic Calculus: Non-Stationary Point of Inflection Example
0:05:04
A-Level Further Maths H1-04 Hyperbolic Functions: Sketching y=tanh(x)
0:02:53
A-Level Further Maths H4-04 Hyperbolic Inverse: Logarithmic Form of y=artanh(x)
0:05:17
A-Level Further Maths H2-05 Hyperbolic Calculus: Integration Examples
0:03:43
A-Level Further Maths H2-03 Hyperbolic Calculus: Tangent Example
0:01:52
A-Level Further Maths H2-01 Hyperbolic Calculus: Differentiating & Integrating sinh(x) and cosh(...
0:05:37
A-Level Further Maths H1-02 Hyperbolic Functions: Sketching y=sinh(x)
0:02:24
A-Level Further Maths H2-06 Hyperbolic Calculus: Part 1 - Definite Integral
0:09:46
A-Level Further Maths H1-05 Hyperbolic Functions: Identities and Osborne’s Rule
0:02:49
AQA A-Level Further Maths H6-04 Hyperbolic Identities: Proof & Equation
0:02:36
A-Level Further Maths H1-06 Hyperbolic Functions: Solve cosh(x)=3sinh(x)-1
0:04:06
A-Level Further Maths H4-05 Hyperbolic Inverse: Solving Equations
0:03:43
A-Level Further Maths H3-01 Hyperbolic Inverse: Sketching y=arsinh(x)
0:04:19
A-Level Further Maths H5-04 Hyperbolic Integration: Definite Integral Examples
0:07:25
A-Level Further Maths H1-01 Hyperbolic Functions: Introduction
0:03:12
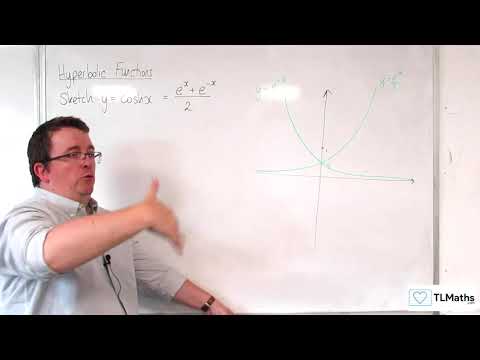
A-Level Further Maths H1-03 Hyperbolic Functions: Sketching y=cosh(x)
0:03:02
A-Level Further Maths H3-02 Hyperbolic Inverse: Sketching y=arcosh(x)
0:02:02
AQA A-Level Further Maths H6-02 Hyperbolic Identities: Prove cosh(2x)=cosh²(x)+sinh²(x)
0:05:47
A-Level Further Maths H4-03 Hyperbolic Inverse: Logarithmic Form of y=arcosh(x)
0:03:25
AQA A-Level Further Maths H6-03 Hyperbolic Identities: Solve 9sinh²(x)+3cosh(x)-101=0
0:03:54
A-Level Further Maths H5-03 Hyperbolic Integration: Indefinite Integral Examples
0:03:08
A-Level Further Maths H5-05 Hyperbolic Integration: Integrate (6x+5)/√(x²-4)
0:00:13
Albert Einstein doing physics | very rare video footage #shorts
0:03:42
OCR MEI MwA E: Minimum Spanning Trees: 01 Introduction & Greedy Algorithms
Комментарии