filmov
tv
Riemann geometry -- covariant derivative

Показать описание
In this video I attempt to explain what a covariant derivative is and why it is useful in the mathematics of curved surfaces. I try to do this using as many visual arguments as possible; however, some knowledge of differential calculus on the part of the viewer is necessary.
Riemann geometry -- covariant derivative
Curvature tensor and Covariant derivative
Tensor Calculus 20: The Abstract Covariant Derivative (Levi-Civita Connection)
Relativity 107b: General Relativity Basics - Manifolds, Covariant Derivative, Geodesics
General Relativity 8-b: Riemann Derived
Tensor Calculus 22: Riemann Curvature Tensor Geometric Meaning (Holonomy + Geodesic Deviation)
What is Riemannain geometry | Riemannian geometry #youtubeshorts #shorts
The Covariant Derivative (Lecture #16b of a course on Relativity & Cosmology)
Differential Geometry in Under 15 Minutes
Infinite-dimensional geometry: Sprays and covariant derivatives vs. weak Riemannian metrics
Lec11 - P2 (Covariant Derivatives, Riemannian Metrics and Geodesics)
Tensor Calculus 18: Covariant Derivative (extrinsic) and Parallel Transport
Tensor Calculus 17: The Covariant Derivative (flat space)
Introduction to Riemannian Geometry - Covariant & Contravariant Vectors
The Covariant Derivative (and Christoffel Terms)
Lecture 1 | Introduction to Riemannian geometry, curvature and Ricci flow | John W. Morgan
What is Riemannian geometry | Riemannian manifold | Riemann Curvature tensor
Lec11 - P1 (Covariant Derivatives, Riemannian Metrics and Geodesics)
Classroom Aid - Riemannian Curvature Tensor
Riemannian Geometry - Definition: Oxford Mathematics 4th Year Student Lecture
Evgeny Malkovich - On the covariant derivative on 3D sub Riemannian Lie groups
Lec11 - P3 (Covariant Derivatives, Riemannian Metrics and Geodesics)
Lec11 - P5 (Covariant Derivatives, Riemannian Metrics and Geodesics)
Relativity 105e: Acceleration - Covariant Derivative in Flat Spacetime (Rindler Coordinates)
Комментарии
 0:10:09
0:10:09
 0:25:13
0:25:13
 0:28:52
0:28:52
 0:36:21
0:36:21
 0:21:21
0:21:21
 0:29:13
0:29:13
 0:00:56
0:00:56
 0:14:26
0:14:26
 0:13:37
0:13:37
 0:26:48
0:26:48
 0:11:13
0:11:13
 0:33:51
0:33:51
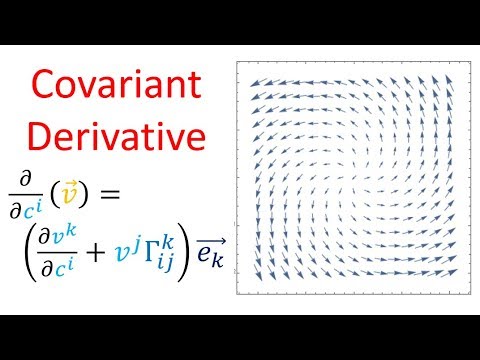 0:18:12
0:18:12
 0:56:02
0:56:02
 0:47:15
0:47:15
 0:58:06
0:58:06
 0:00:59
0:00:59
 0:18:47
0:18:47
 0:06:14
0:06:14
 0:20:18
0:20:18
 0:29:13
0:29:13
 0:18:53
0:18:53
 0:18:39
0:18:39
 0:27:17
0:27:17