filmov
tv
EE 503 : Lecture 21 (Fall 2020, METU)
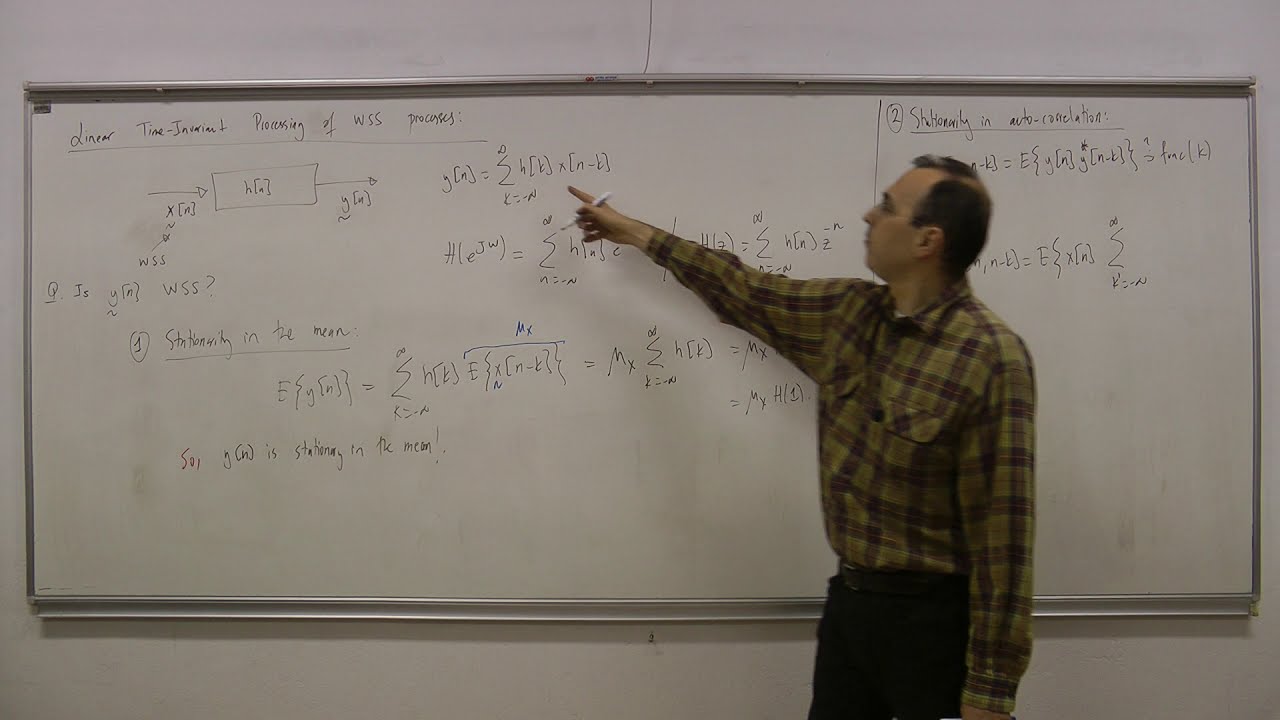
Показать описание
EE 503 - Statistical Signal Processing and Modeling
Fall 2020, Middle East Technical University, Ankara, Turkey.
Instructor: Prof. Cagatay Candan
Lecture 21
Lecture Contents:
0:00 - Auto-correlation calculation, (LTI processing of WSS processes)
0:58 - Step 1: Cross-correlation calculation (auto-correlation calculation)
7:34 - Step 2: Auto-correlation calculation (auto-correlation calculation)
11:54 - Power spectral density
14:46 - Evaluation of output auto-correlation and input-output cross-correlation with Fourier transform
15:50 - DTFT of conj( h[ -n ] )
19:53 - Output power spectral density relations in Fourier-domain
22:30 - Z transform of conj( h[ -n ] )
27:00 - Output power spectral density relations in z-domain
30:28 - H(z) and H^*(1/z^*); conjugate reciprocal pole/zero pairs
40:57 - Power Spectral Density (properties)
41:00 - Property 1: Power spectral density is real valued
44:25 - Property 2: Power spectral density is non-negative (proved later)
44:48 - Property 3: Area under power spectral density is r_x[0] = E{ | x[n] |^2 }
Fall 2020, Middle East Technical University, Ankara, Turkey.
Instructor: Prof. Cagatay Candan
Lecture 21
Lecture Contents:
0:00 - Auto-correlation calculation, (LTI processing of WSS processes)
0:58 - Step 1: Cross-correlation calculation (auto-correlation calculation)
7:34 - Step 2: Auto-correlation calculation (auto-correlation calculation)
11:54 - Power spectral density
14:46 - Evaluation of output auto-correlation and input-output cross-correlation with Fourier transform
15:50 - DTFT of conj( h[ -n ] )
19:53 - Output power spectral density relations in Fourier-domain
22:30 - Z transform of conj( h[ -n ] )
27:00 - Output power spectral density relations in z-domain
30:28 - H(z) and H^*(1/z^*); conjugate reciprocal pole/zero pairs
40:57 - Power Spectral Density (properties)
41:00 - Property 1: Power spectral density is real valued
44:25 - Property 2: Power spectral density is non-negative (proved later)
44:48 - Property 3: Area under power spectral density is r_x[0] = E{ | x[n] |^2 }
 0:50:56
0:50:56
 0:27:55
0:27:55
 0:27:55
0:27:55
 1:13:34
1:13:34
 1:08:15
1:08:15
 0:41:28
0:41:28
 0:55:31
0:55:31
 1:02:21
1:02:21
 1:04:03
1:04:03
 0:59:12
0:59:12
 1:05:22
1:05:22
 1:06:44
1:06:44
 1:17:34
1:17:34
 1:03:24
1:03:24
 1:00:10
1:00:10
 1:01:33
1:01:33
 0:57:26
0:57:26
 0:56:12
0:56:12
 1:04:37
1:04:37
 1:03:42
1:03:42
 1:01:43
1:01:43
 0:45:54
0:45:54
 0:21:52
0:21:52
 1:16:56
1:16:56