filmov
tv
Year 13/A2 Pure Chapter 11.12 (Integration)
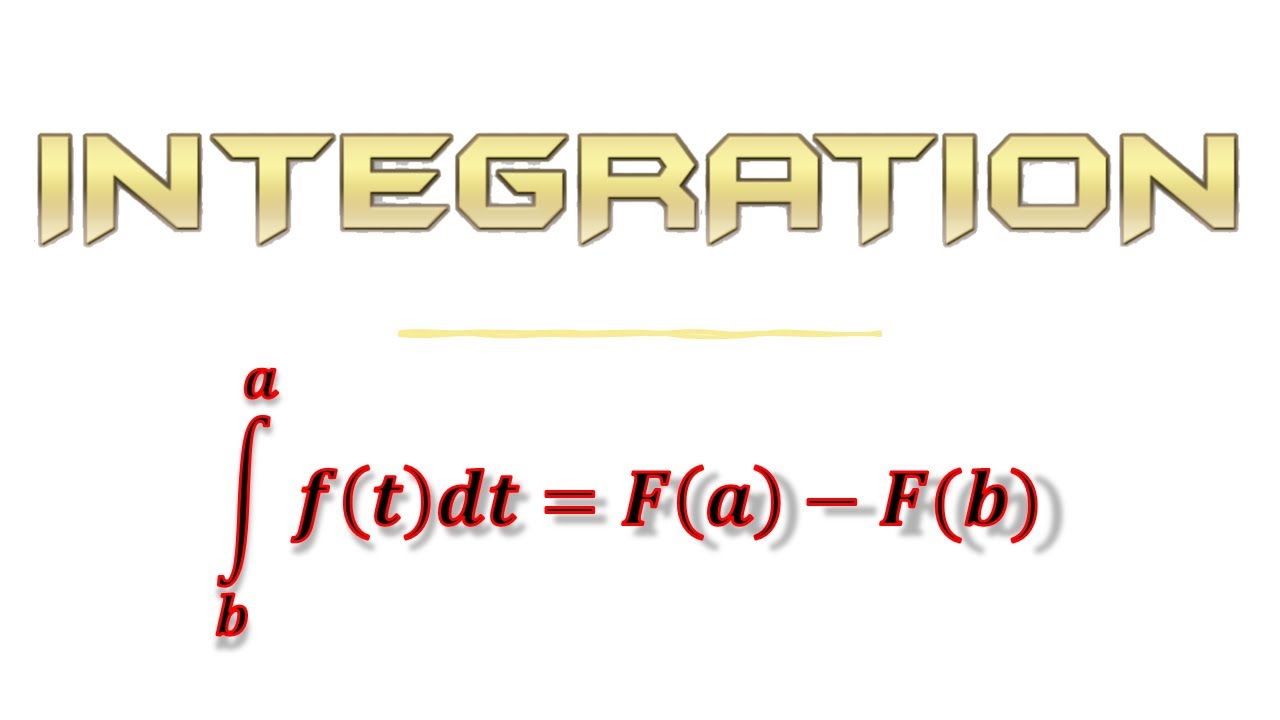
Показать описание
Welcome to the end of integration...sort of!
This is where the course leaves integration, but I'll be doing an extra session involving knowing how to select which method of integration to use when faced with an unfamiliar integral.
However, for now, this video briefly examines summation notation for integrals, and uses the general result that, for f(𝑥) continuous on the interval 𝑎 ≤ 𝑥 ≤ 𝑏, then (lim 𝑥 ⮕ 0) Σf(𝑥)δ𝑥 = ∫f(𝑥)d𝑥, for that interval.
Robustly roving this result in the beyond the scope of thw course (and beyond my ability 😂), but I do mention how we could hypotethically prove the result when integrating algebraic integer powers (for example, integrating ∫𝑥³d𝑥. I do this by adapting from the Riemann integral, and have called this Integration (of f(𝑥) = 𝑥³) From First Principles.
Sadly, but totally understandably, the course doesn't delve into illustrative examples of such beautiful results, so I've put this to one side as optional, in case you're interested.
FYI: Integration From First Principles example:
This lesson is meant as preparation for Exercise 11L, page 330 of the Pearson Edexcel Pure Mathematics Year 2/A2 Textbook.
Introduction: 0:00
Solution to Warm-Up Q1: 1:23
Solution to Warm-Up Q2: 12:03
INTEGRATION AS THE LIMIT OF A SUM
Introduction: 19:41
Worked Example: 24:00
Suggested Exercises: 28:37
This is where the course leaves integration, but I'll be doing an extra session involving knowing how to select which method of integration to use when faced with an unfamiliar integral.
However, for now, this video briefly examines summation notation for integrals, and uses the general result that, for f(𝑥) continuous on the interval 𝑎 ≤ 𝑥 ≤ 𝑏, then (lim 𝑥 ⮕ 0) Σf(𝑥)δ𝑥 = ∫f(𝑥)d𝑥, for that interval.
Robustly roving this result in the beyond the scope of thw course (and beyond my ability 😂), but I do mention how we could hypotethically prove the result when integrating algebraic integer powers (for example, integrating ∫𝑥³d𝑥. I do this by adapting from the Riemann integral, and have called this Integration (of f(𝑥) = 𝑥³) From First Principles.
Sadly, but totally understandably, the course doesn't delve into illustrative examples of such beautiful results, so I've put this to one side as optional, in case you're interested.
FYI: Integration From First Principles example:
This lesson is meant as preparation for Exercise 11L, page 330 of the Pearson Edexcel Pure Mathematics Year 2/A2 Textbook.
Introduction: 0:00
Solution to Warm-Up Q1: 1:23
Solution to Warm-Up Q2: 12:03
INTEGRATION AS THE LIMIT OF A SUM
Introduction: 19:41
Worked Example: 24:00
Suggested Exercises: 28:37
 0:29:30
0:29:30
 1:01:56
1:01:56
 1:13:10
1:13:10
 0:53:37
0:53:37
 0:42:09
0:42:09
 0:22:33
0:22:33
 3:02:38
3:02:38
 0:54:12
0:54:12
 0:35:28
0:35:28
 0:37:14
0:37:14
 1:01:02
1:01:02
 0:43:21
0:43:21
 0:56:56
0:56:56
 0:57:33
0:57:33
 0:00:34
0:00:34
 1:02:19
1:02:19
 0:00:14
0:00:14
 0:40:40
0:40:40
 0:00:11
0:00:11
 0:04:19
0:04:19
 0:00:15
0:00:15
 0:00:12
0:00:12
 0:00:13
0:00:13
 0:00:19
0:00:19