Quantum field theory, Lecture 5

This winter semester (2016-2017) I am giving a course on quantum field theory. This course is intended for theorists with familiarity with advanced quantum mechanics and statistical physics. The main objective is introduce the building blocks of quantum electrodynamics.

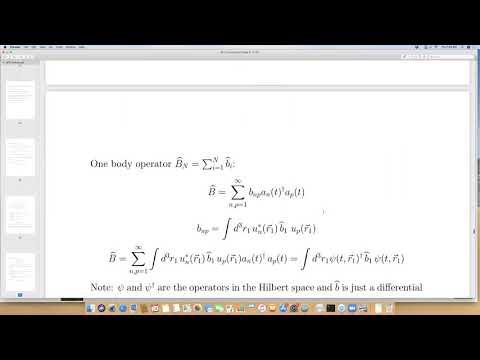
Here in Lecture 5 I begin the argument that the quantum Klein-Gordon field is a relativistic quantum theory.

[mattmolewski]

If your party doesn't have a projective unitary representation of the Poincare group, don't even invite me.

[caykroyd]

It took me a moment to understand how the |p> state normalization stems from the single particle projector. We found the factor X(p) that makes the measure invariant, and therefore also makes the term |p> <p| in the integral invariant. Now we know that X(p) |p> <p| is invariant and that can only be true if \sqrt{X(p)} |p> is invariant as well!
Correct me if I'm wrong, thanks!

[lorenzomagro]

Dear prof. Tobias Osborne i am following your lessons in QFT and I must say that are very precise and rigorous. If i find any errors or deficiencies I report you Thanks again for your work and for the beautiful physical channel. I hope that you post the exercises of QFT.
L. Magro Italy

[PeeterJoot]

I'm amazed that not of the in-class students ask any questions, especially for a subject like this. Are they camera shy, or super polite (to their own detriment?)

[anthonybrady]

Minor correction. You briefly mentioned 10 generators/charges of Poincaré group. Then said “no, there are 14”. The former was correct however. The Poincaré group=10 parameter continuous group, implying 10 conserved charges associated with 3 boosts + 3 rotations + 4 spatiotemporal translations. Cheers.

[javierrendon]

Hi professor Osborne, in 12:56 you mentioned first 10 generators (which is good) and then 14 generators for the poincaré group, I know it is just irrelevant in the context (you worked out the full 10 conserved charges in lecture 4), but I wanted to pointed out that. By the way what an amazing course. I hope you give a lecture on statistical mechanics or GR in the near future.

[DaytonaStation]

Also as a retired lecturer myself I appreciate good blackboard organization and clear and quick handwriting. It pains me to listen to Leonard.

[jonlasa]

Amazing funny comments Tobias, love your classes! Thank you :)

[achiltsompanos]

Dear prof. Osborne I have to questions:
1. Why is important to find "unitary projective reps of the Poincare group"?
2. I noticed that you hint sometimes at a deeper level of mathematical connections with measure theory (maths) when you speak for example about measurable functions. I would like to see this connections visited some more, possibly in an origins spin off!!.
In math when you consider non measurable sets and uncountable unions of sets all hell breaks loose and non "classical" things happen. I was always wondering if there is a connection with quantum mechanics there but as you say I wouldn't suggest this as a research project...

Many thanks.
Achilleas

[filifur]

First of all, thank you for your videos and for shearing them with the world, in several of the characteristics of the space you work in, you ask for it to be measurable, any good reference books on measure theory for physics?, thanks again

[jimmyb]

1:03:23; I suspect you meant the commutators with the CREATION operator, a^+_p. Indeed in the corollary, when working out P^\mu | p_1, ... >, you want to move CREATION operators past P^\mu.

[tiamatbenoit]

Dear professor, if you could teach general relativity. Your lessons are for a much more rigorous mathematician than I have sometimes been able to study from books and lessons given by physicists. Thank you

[jimmyb]

31:13 Hilbert space is builT, with a t ;)

[DaytonaStation]

lectures started off slow ....then got great. you need to give them to prof Zee ... he gave up on trying to make qft lectures

[zoltankurti]

46:00 I don't see how this is invariant. Are we supposing here that the particle number stays the same all the time? Because if particles can come and go at different places, I can very easily imagine a lorentz boost messing up the particle number.

[sdu]

How did we get to the equality at 55:45, how did we get 2p_0 in the denominator? Also, the L.H.S. is the total 4-momentum, whereas, R.H.S. is the total 3-momentum. How can 2 different quantities be equated?
Why has the vacuum state been referred to as the "highest wave vector" in the lecture? Thanks

[caverac]

Prof. Osborne, thanks once again for sharing these lectures, they are great. At about 1:21:21, shouldn't the normalization of the four-momentum operator include a (2pi)^{3/2}?

[joaoafonsojantarada]

Good evening, ProfºTobias Osborne. I am a portuguese student of the master course in particle physics and quantum field theory. My dout is this: I don´t know how the creation and anniquilation opperators appers from a fourier transfor of the phi(x). Can you help me? Thank you in advance

[j.cottner]

I enjoy the mysteries of the quantum world so much that I was inspired to write a fiction novel about it called Quantum Bob:

[orionexploding]

Many thanks to Tobias Osborne for making these lectures available to everyone. Trying to learn QFT is my retirement project and I'm finding the textbooks hard going. These lectures are filling in a lot of the gaps for me.

I must say though, the students must all be geniuses, as they never seem to have any questions. If I was sitting in there I'd be constantly plaguing Tobias with questions.