A relativistic electromagnetism example

This video shows an example of a particle moving in a uniform electric field.

1. First we use the classical law of motion: F=ma. According to this law uniform force means uniform acceleration, and the particle can reach the speed of light, and continue to accelerate. According to relativity, this can't be true.

2. The classical law can also be formulated: F=d/dt mv. Meaning: the change of momentum is proportional to the force. This works also in relativity, only this time the mass m is changing. It grows as the velocity grows. This makes it harder for it to increase its velocity further. This prevents it from ever reaching the speed of light.

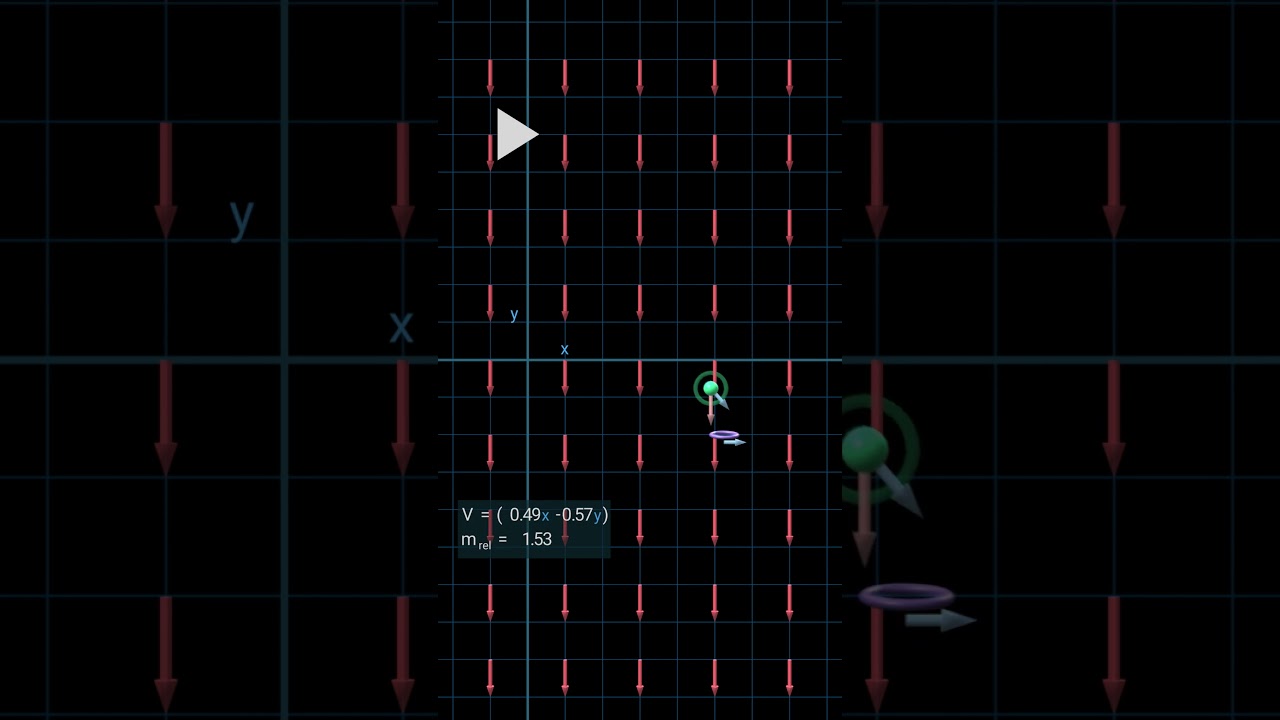
3. Now we switch to a different point of view: an observer moving at 60% the speed of light to the left. This observer views the same scene, but from this point of view the particle and the hoop have an initial velocity of 60% the speed of light to the right. If we used the F=ma law, then the particle would have accelerated downwards, while v_x would remain at a steady 0.6. But with the relativistic law something different happens: the x momentum, m v_x, remains constant, because there's no force along the x direction. But m grows, so it means v_x diminishes. The hoop however floats steadily at 0.6, so the particle falls short. This can't be true of course, the second observer is watching the same scene: the particle should pass through the hoop.

4. The 4th scene fixes that. According to relativity, when we switch between points of view we should transform the electromagnetic field. In our example, this means the electric field grows by 25%, and a magnetic field shows up. The 'x' marks shown in the video are a common convention for a vector field pointing into the screen, along a Z axis that is not shown. The magnetic force is perpendicular to the magnetic field and to the particle's velocity. It provides just the right amount of pull along the x-axis to keep v_x steady.

5. The 5th scene is a sneak peek into visualization of tensors part 2, due in August.

[twixerclawford]

It breaks my brain that all the laws of physics seem to just perfectly align to keep everything consistent

[AgentMidnight]

I was not prepared for the psychic damage when it jumped to the third dimension

[drdca]

My impression is most physicists avoid using the concept of relativistic mass? Instead just saying that instead of F = m a, instead (I think?) saying that net force is the rate of change of momentum, and that the momentum is not just m v, but instead has the relativistic stuff in the momentum, rather than in the mass. For one thing, if you had relativistic mass, it would be different in different directions?

[Darthvanger]

Waiting so much for the tensor explanation! My teacher once said that magnetism is just the relativistic effect, and I was dazzled ever since! I didn't understand shit in that course in university :D

[floppy]

FINALLY, ANOTHER VIDEO and it's a short

[pavelrozhkov]

Oh god no, don't use relativistic mass in explanations. This term is outdated and only leads to more misunderstanding.

[vivekpanchal]

Hey, next please simulate, A charged particle on the axis that passes through a ring with uniform linear charge density, neglecting friction and other effects like induction or anything, considering friction at the end the particle will stay at the centre, ideally

One professor showed in a lecture that, Particle will oscillate and the total energy is conserved, and it is equivalent to what happen if we ideally put a charge in cavity of conductor, the charges inside matter of the cavity will feel the same process until equilibrium is arrived due to collision and considering friction.

[JP-ivme]

"it will never reach the speed of light" :( c'mon its trying its best

[samsara]

And.. is everything is relative.. how do you know is going 60% of the speed of light? 60% relative with what?

[idiotsgame]

so can I imagine the hoop as an electrical wire? the particle will be an amp I quess

[adriannuske]

This, although sounds wise.and.misterious, is counterintuitive. It's better to say that the space compresses in.fron of it.and becomes thicker to infinity (or a very hight value as it.aproaches the speed of light) also this is more like what happens in reality.

[Fabrizio_Ruffo]

If it gains mass, why doesn't it gain weight?

[PeterBaumgarta]

Except that there is no "relativistic mass, " most serious physicists avoid the concept.