filmov
tv
Solving Exponential Equations Reducible to Quadratics

Показать описание
#quadraticequations #exponentialequations #quadratics
In this video, we look at how to solve exponential equations that are reducible to quadratic equations.
In general, to reduce an exponential equation to a quadratic equation, we use the index law to modify one of the terms to a common prime base.
We then make the u-substitution to reduce it to a quadratic which then an be solved using any of the methods - PSF (Product Sum Factors) factorising method, completing the square or quadratic formula.
The examples in this video are, solve:
4^x - 9*(2^x) + 8 = 0
9^x - 26(3^x) - 27 = 0
In this video, we look at how to solve exponential equations that are reducible to quadratic equations.
In general, to reduce an exponential equation to a quadratic equation, we use the index law to modify one of the terms to a common prime base.
We then make the u-substitution to reduce it to a quadratic which then an be solved using any of the methods - PSF (Product Sum Factors) factorising method, completing the square or quadratic formula.
The examples in this video are, solve:
4^x - 9*(2^x) + 8 = 0
9^x - 26(3^x) - 27 = 0
 0:07:58
0:07:58
 0:07:29
0:07:29
 0:02:26
0:02:26
 0:21:15
0:21:15
 0:14:12
0:14:12
 0:06:50
0:06:50
 0:03:13
0:03:13
 0:08:19
0:08:19
 0:10:40
0:10:40
 0:11:16
0:11:16
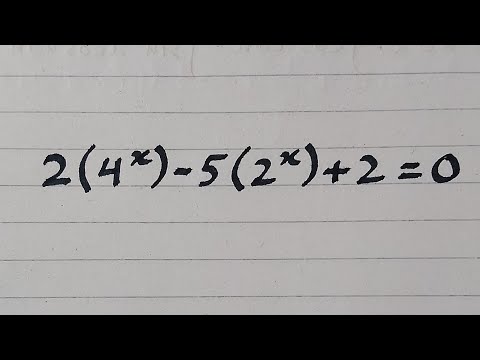 0:03:01
0:03:01
 0:29:53
0:29:53
 0:06:06
0:06:06
 0:02:57
0:02:57
 0:05:52
0:05:52
 0:08:17
0:08:17
 0:01:57
0:01:57
 0:13:21
0:13:21
 0:02:34
0:02:34
 0:19:19
0:19:19
 0:02:18
0:02:18
 0:12:58
0:12:58
 0:03:05
0:03:05
 0:07:04
0:07:04