filmov
tv
Math Olympiad - Exponential Trigonometric Problem - find x!
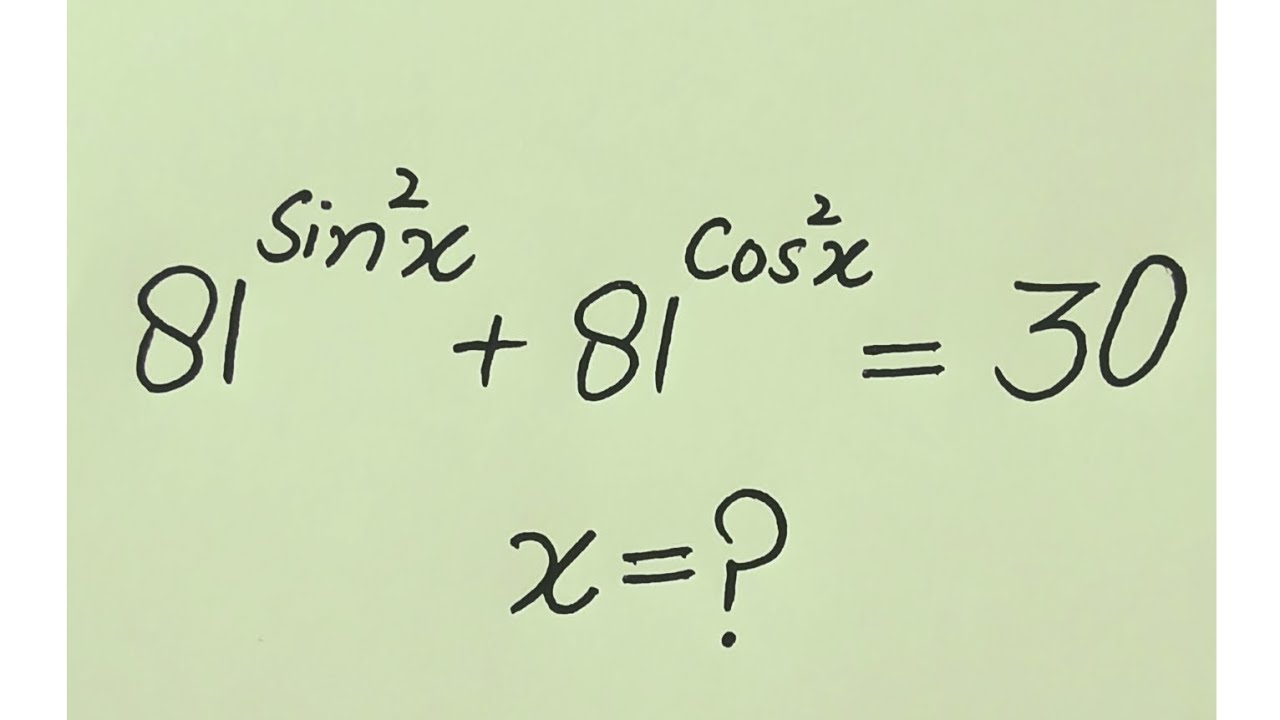
Показать описание
Math Olympiad - Exponential Trigonometric Problem - find x! #matholympiad #maths #matholympics #mathcompetition #mathematics #mathcontest #education #mathstricks #mathstricks #trigonometry #solution #equation
Math Olympiad Question | Solving an Exponential Trigonometric Equation | Can You Solve?!
Solving an Olympiad Trigonometric Exponential Equation #math
An Exponential Trigonometric Equation | Math Olympiads
A Trigonometric Exponential Equation with Sine and Cosine | Math Olympiad | Algebra
Fascinating Olympiad Trigonometric Exponential Equation
How to Solve the Mixed Exponential and Trigonometric Equation? | Math Olympiad
A Nice Olympiad Exponential Trigonometric Problem || Math Olympiad ||
Math Olympiad - Exponential Trigonometric Problem - find x!
Maths Olympiad Problem | An Exponential Equation
Math Olympiad questions | Trigonometric Equations | Find X | Height and Distance
A Brilliant Olympiad Exponential Equation in Trigonometric Form @mathsmood
A Nice Olympiad Trigonometric Exponential Equation | Geendle
A Nice Olympiad Trigonometric Exponential Equation
Solve the Trigonometric Equation for X | Answer in Degrees and Radians | Math Olympiad Training
Solving Trigonometric Equation | Win Math Olympiad
Germany l can you solve this Exponential Trigonometric problem l Olympiad Math.
Can you solve this Olympiad problem || Math Olympiad || Trigonometry
Olympiad Trigonometric Exponential Equation 💪💪 | Olympiad Math 🎉🎉🎉
Solving For x #shorts #short #maths #exponents #mathstricks #mathematics #viral #math #olympiad
A Nice Math Olympiad Trigonometric Problem
Exponential Function Involving Trigonometry | Nice Exponential Equation | Math Olympiad
Nice! Olympiad Maths | Trigonometry exponential equation
Olympiad Maths for Class 11 | Can You Solve This Exponential Trigonometric Equation @mathsmood
#basic #trigonometry #problem #maths #olympiad #sat
Комментарии
 0:05:50
0:05:50
 0:08:57
0:08:57
 0:08:24
0:08:24
 0:07:39
0:07:39
 0:09:56
0:09:56
 0:03:48
0:03:48
 0:07:05
0:07:05
 0:15:25
0:15:25
 0:03:31
0:03:31
 0:07:28
0:07:28
 0:10:29
0:10:29
 0:07:43
0:07:43
 0:09:44
0:09:44
 0:10:48
0:10:48
 0:03:15
0:03:15
 0:15:13
0:15:13
 0:06:31
0:06:31
 0:10:25
0:10:25
 0:01:01
0:01:01
 0:13:13
0:13:13
 0:09:41
0:09:41
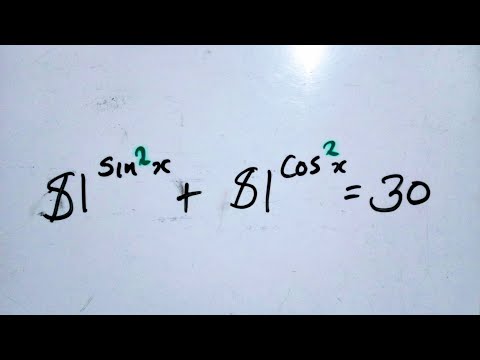 0:11:15
0:11:15
 0:06:39
0:06:39
 0:00:46
0:00:46