filmov
tv
How to verify a trigonometric identity by simplifying a complex fraction

Показать описание
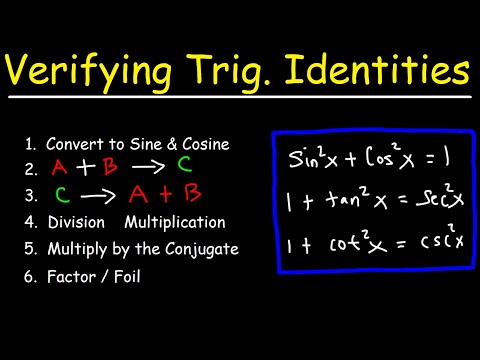
👉 Learn how to verify trigonometric identities having rational expressions. To verify trigonometric expression means to verify that the term(s) on the left hand side of the equality sign is equal to the term(s) on the right hand side. To verify rational trigonometric identities, it is usually more convenient to start with getting rid of the denominator(s) of the rational term(s). This can be done by multiplying both the numerator and the denominator by the conjugate if the denominator involves addition/subtraction or by the reciprocal if the denominator involves product.
For non-rational trigonometric identities, we can replace given trigonometric functions/identities with equivalent trigonometric functions/identities and evaluate accordingly.
Organized Videos:
✅ Verify Trigonometric Identities
✅ Verify Simple Trigonometric Identities
✅ Verify Trigonometric Identities with Rational Expressions
✅ Verify Trigonometric Identities by Multiplying
✅ Verify Trigonometric Identities by Adding and Subtracting
✅ Verify Trigonometric Identities with Fractions
✅ Verify Trigonometric Identities by Pythagorean Identities
Connect with me:
#analytictrig #brianmlogan
For non-rational trigonometric identities, we can replace given trigonometric functions/identities with equivalent trigonometric functions/identities and evaluate accordingly.
Organized Videos:
✅ Verify Trigonometric Identities
✅ Verify Simple Trigonometric Identities
✅ Verify Trigonometric Identities with Rational Expressions
✅ Verify Trigonometric Identities by Multiplying
✅ Verify Trigonometric Identities by Adding and Subtracting
✅ Verify Trigonometric Identities with Fractions
✅ Verify Trigonometric Identities by Pythagorean Identities
Connect with me:
#analytictrig #brianmlogan
Комментарии
 0:05:12
0:05:12
 0:24:51
0:24:51
 0:04:57
0:04:57
 0:04:13
0:04:13
 0:00:59
0:00:59
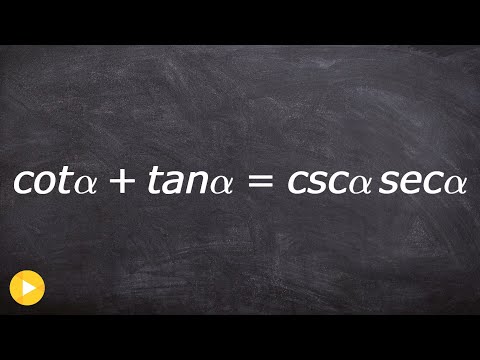 0:04:17
0:04:17
 0:01:36
0:01:36
 0:19:53
0:19:53
 0:06:46
0:06:46
 0:07:37
0:07:37
 0:04:36
0:04:36
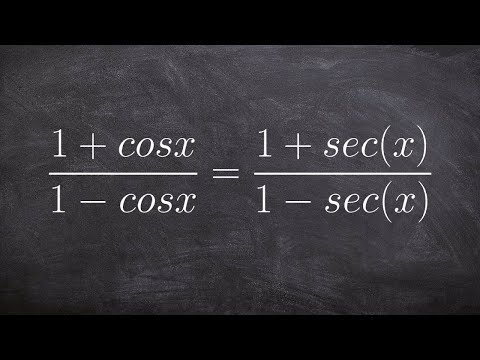 0:07:26
0:07:26
 0:06:53
0:06:53
 0:01:59
0:01:59
 0:01:41
0:01:41
 0:05:16
0:05:16
 0:06:35
0:06:35
 0:02:21
0:02:21
 0:25:08
0:25:08
 0:03:03
0:03:03
 0:09:14
0:09:14
 0:01:38
0:01:38
 0:00:56
0:00:56
 0:04:22
0:04:22