301.10C Group Homomorphism: Definition and Example

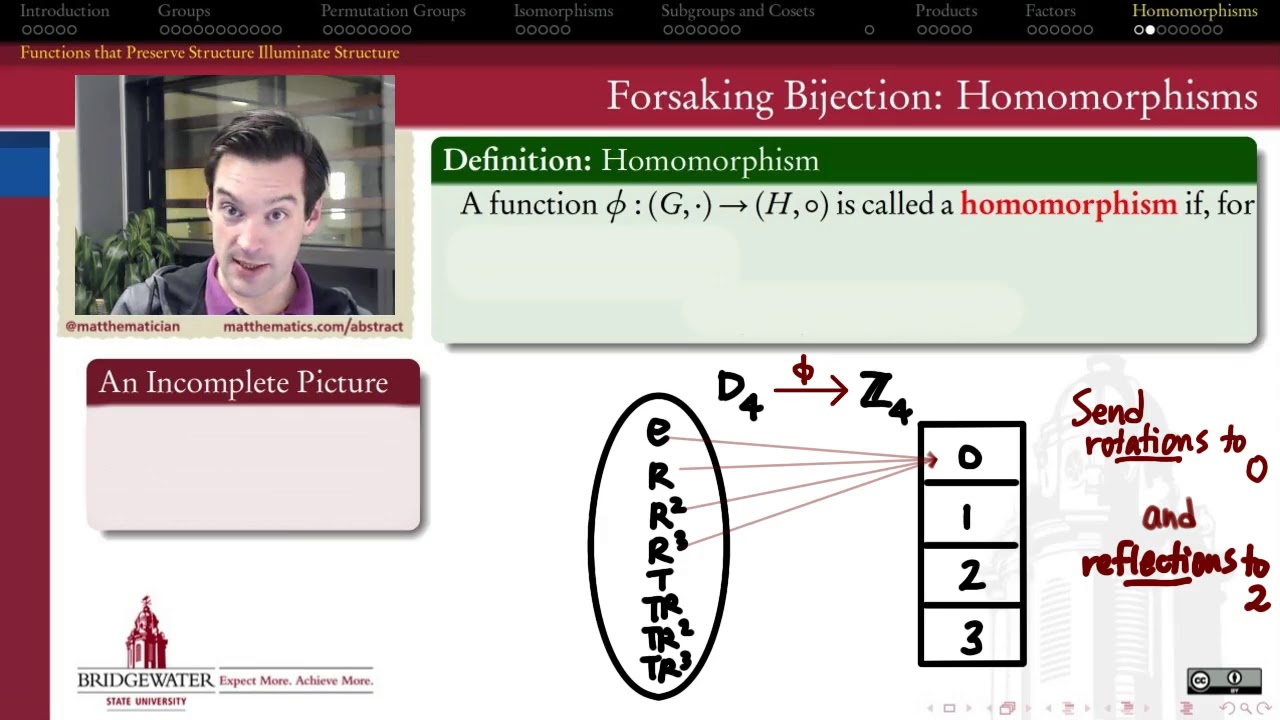
A homomorphism of groups is an "isomorphism that might not be a bijection." Because it preserves the structure of its domain group, it has the power to illuminate the structure of that group -- here's a motivating example using a homomorphism from D4 to Z4.

[PunmasterSTP]

Exploring groups like this and just trying to see what you *might* be able to do is so fun!

[billhalprin]

I have three difficulties with this lecture: 1) T, TR, TRR, and TRRR are not reflections in the sense of Gallian's H, V, D and D prime reflections; they are only reflections back and forth around the vertical axis (see the Dihedral Group Explorer); 2) the homomorphism structure, requiring a functional transaction between D4 to Z4, does not rise above mirror image functions carried out separately in D4 and Z4; and 3) the conclusion as to the separateness of rotations and reflections is apparent from the start.

[hyperduality]

Absolute truth is dual to relative truth -- Hume's fork.
Homomorphisms (similarity, relative) are dual to isomorphisms (same, absolute).
A priori (before, group or domain) is dual to a posteriori (after, image or codomain) -- Immanuel Kant.
Injective is dual to surjective synthesizes bijective or isomorphism.
"Always two there are" -- Yoda.

[billhalprin]

Please disregard my below comment. I was incorrect.