filmov
tv
Denis-Charles Cisinski, Univalence of the universal coCartesian fibration

Показать описание
Homotopy Type Theory Electronic Seminar Talks, 2020-04-02
The model of higher categories given by Joyal's model structure for quasi-categories has univalent universes of coCartesian fibrations. This subsumes the existence of univalent universes of Kan fibrations proved by Voevodsky. Furthermore, the existence of such universes can be used as an alternative to the yoga of homotopy coherent nerves to prove all the essential features of higher category theory, giving a (directed) type theoretic approach to the foundations of higher categories.
The model of higher categories given by Joyal's model structure for quasi-categories has univalent universes of coCartesian fibrations. This subsumes the existence of univalent universes of Kan fibrations proved by Voevodsky. Furthermore, the existence of such universes can be used as an alternative to the yoga of homotopy coherent nerves to prove all the essential features of higher category theory, giving a (directed) type theoretic approach to the foundations of higher categories.
Denis-Charles Cisinski, Univalence of the universal coCartesian fibration
Denis-Charles Cisinski. Homological decomposition and motives.
Cisinski, Nguyen, Walde: Univalent Directed Type theory, Part 1
Cisinski, Nguyen, Walde: Univalent Directed Type theory, Part 3
Cisinski, Nguyen, Walde: Univalent Directed Type theory, Part 2
Bourbaki - 21/03/15 - 3/3 - Denis Charles CISINSKI
My favourite K-theory fact
Matthew Weaver, A constructive model of directed univalence in bicubical sets
From Scratch to Univalence | #SoME2
Hoang Kim Nguyen, Directed univalence in simplicial sets
Higher Categories reading group - talk 2 (08/13/22)
Intensionality, Invariance, and Univalence, Steve Awodey
Rasekh - Fibrations of (oo,n)-Categories
Higher Categories reading group - talk 9 (10/01/22)
Andrew Pitts, Axiomatizing cubical sets models of univalent foundations
E5.E – A Constructive Model of Directed Univalence in Bicubical Sets
Chris Grossack, Where are the open sets? Comparing HoTT with Classical Topology
Brandon Doherty, Cubical models of (∞,1)-categories
Denis Nardin - A description of the motive of Hilb(A∞)
La Révolution des Damnés, entretien avec Melody Cisinski
La Révolution des Damnés (Roman Graphique) - Interview de Mélody Cisinski
Charles Denis Bourbaki
[Day 1] Minicourse: Effective methods in PI-theory II - Vladimir Dotsenko
André Joyal - Higher sheaves
Комментарии
 1:11:38
1:11:38
 1:11:05
1:11:05
 1:43:20
1:43:20
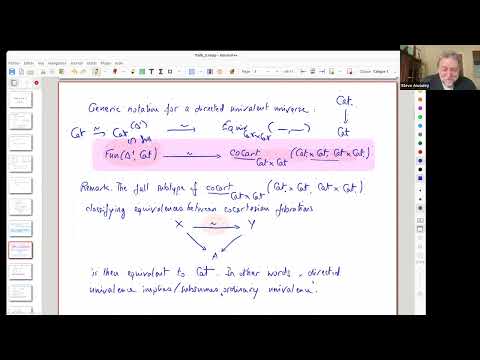 2:13:08
2:13:08
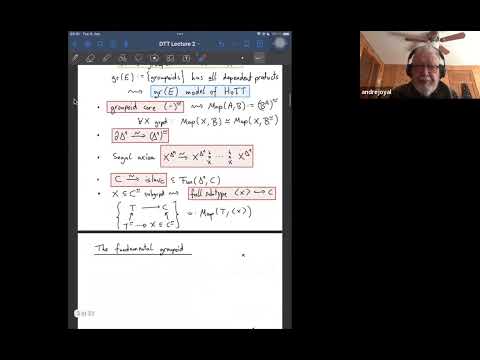 2:10:22
2:10:22
 1:17:37
1:17:37
 0:09:06
0:09:06
 0:45:45
0:45:45
 0:20:37
0:20:37
 1:08:15
1:08:15
 1:15:17
1:15:17
 0:56:52
0:56:52
 0:10:01
0:10:01
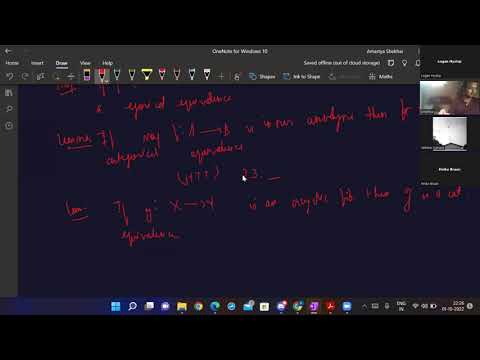 1:03:52
1:03:52
 1:23:43
1:23:43
 0:26:31
0:26:31
 0:38:06
0:38:06
 0:51:47
0:51:47
 1:22:12
1:22:12
 0:18:35
0:18:35
 0:07:09
0:07:09
 0:04:31
0:04:31
![[Day 1] Minicourse:](https://i.ytimg.com/vi/dbJ66RBFzJs/hqdefault.jpg) 1:03:36
1:03:36
 1:10:39
1:10:39