filmov
tv
8 класс, 33 урок, Основная теорема арифметики натуральных чисел. Решение задач на делимость

Показать описание
Решаем задачи (упражнения) на заказ (!).
.
Для студентов - математический анализ, линейная алгебра, аналитическая геометрия итд...
Для школьников - математика (алгебра, геометрия), физика, химия.
.
Примерное время ожидания заказа - 10 минут
.
.
Реквизиты:
KASPI GOLD: +7 (705) 434 41 44, Молдiр О.
БАНКОВСКИЙ ПЕРЕВОД: 4400 4301 5438 5790 MOLDIR OMIRALI
.
.
Для студентов - математический анализ, линейная алгебра, аналитическая геометрия итд...
Для школьников - математика (алгебра, геометрия), физика, химия.
.
Примерное время ожидания заказа - 10 минут
.
.
Реквизиты:
KASPI GOLD: +7 (705) 434 41 44, Молдiр О.
БАНКОВСКИЙ ПЕРЕВОД: 4400 4301 5438 5790 MOLDIR OMIRALI
.
8 класс, 33 урок, Основная теорема арифметики натуральных чисел. Решение задач на делимость...
Квадратные уравнения. Основные понятия | Алгебра 8 класс #33 | Инфоурок...
Количество вещества. Моль. Число Авогадро. 8 класс.
Габриелян О. С. 8 класс §33 'Реакции обмена'.
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnline...
Математика это не Ислам
УРОК 33. Использование стилей (8 класс)
Задание №33 – Гдз по алгебре 8 класс (Макарычев)
Удалили с экзамена ОГЭ Устное Собеседование shorts #shorts
9 класс, 33 урок, Основные характеристики гармоничных колебаний...
ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!
Сократить дробь алгебра 8 класс
Шахтёр жил 17 лет под землёй и вот что с ним стало😨 #история...
Реакция на результаты ЕГЭ 2022 по русскому языку
Как умножать сложные числа? Лайфхак👌 #shorts
Трапеция. 8 класс.
Электрическая цепь и ее составные части. Сила тока. Напряжение. 8 класс....
Делаю уроки по чистописанию. Урок 33, класс 1: буквы З, Я
Проверь свои знания по математике за 11 класс
10 класс, 33 урок, Правильная пирамида
Ковалентная связь. 8 класс.
мотивация учить английский
Самые высокооплачиваемые профессии💗😩
Урок ИЗО в школе. 8 класс. Урок № 33. «Мультипликационный фильм»....
Комментарии
 0:02:16
0:02:16
 0:13:03
0:13:03
 0:11:06
0:11:06
 0:11:31
0:11:31
 0:07:45
0:07:45
 0:00:21
0:00:21
 0:17:09
0:17:09
 0:07:01
0:07:01
 0:00:24
0:00:24
 0:03:36
0:03:36
 0:00:54
0:00:54
 0:06:39
0:06:39
 0:00:56
0:00:56
 0:00:13
0:00:13
 0:00:59
0:00:59
 0:08:26
0:08:26
 0:10:41
0:10:41
 0:39:09
0:39:09
 0:00:18
0:00:18
 0:07:12
0:07:12
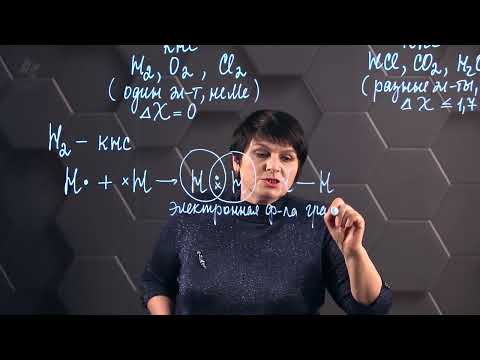 0:13:09
0:13:09
 0:00:16
0:00:16
 0:00:15
0:00:15
 0:20:42
0:20:42