filmov
tv
11 The excision axiom

Показать описание
This is episode 11 of a course on algebraic topology.
We motivate the proof of the excision axiom for singular homology. Proof details are given modulo a proof of the lemma of small simplices.
Outline:
00:00 Start
02:26 Def.: 𝒰-small
07:32 Lemma of small simplices
10:35 Proof of excision axiom based on the lemma of simplices
25:06 Idea of the lemma of small simplices
We motivate the proof of the excision axiom for singular homology. Proof details are given modulo a proof of the lemma of small simplices.
Outline:
00:00 Start
02:26 Def.: 𝒰-small
07:32 Lemma of small simplices
10:35 Proof of excision axiom based on the lemma of simplices
25:06 Idea of the lemma of small simplices
11 The excision axiom
Excision, applications (part 1)- Homology of quotients
04 Eilenberg-Steenrod Axioms
05 Homology of spheres from the axioms
Excision, applications (part 2)- Homology group of Spheres
13 The dimension axiom
Homotopy extension property theorem part 2
6802 Excision and Freudenthal Suspension Theorem
L15 - Proof of the Excision Theorem
Algebraic Topology: L11, homology, 9-29-16, part 2
06 Exemplary computation of an induced map
Algebraic Topology: 11-29-16 part 1
Measure Theory 11 - Open sets are relatively additive
12 The lemma of small simplices
INF1N1TE & Chromixe - Axiom
08 The long exact sequence axiom in homology
Measure Theory 12 - Closed sets are relatively additive
Highlights of Simplicial Homology
Excision Theorem and Degree of a Map
EXCISION - BOUNCE - LIVE IN CALGARY (2014)
17 The triple sequence
Antonio Rieser (03/29/23): Algebraic Topology for Graphs and Mesoscopic Spaces
NFG Talents Mix 012 by Impak + FREE RELEASE
Spor - SUPERNOVA (Original Version, Lifted)
Комментарии
 0:47:07
0:47:07
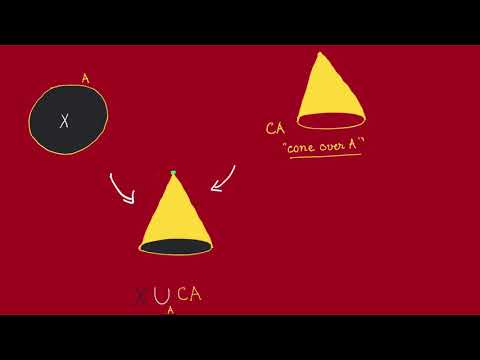 0:04:27
0:04:27
 0:30:55
0:30:55
 0:44:52
0:44:52
 0:04:26
0:04:26
 0:07:22
0:07:22
 0:00:24
0:00:24
 1:06:19
1:06:19
 1:19:08
1:19:08
 0:10:50
0:10:50
 0:25:51
0:25:51
 0:59:51
0:59:51
 0:21:40
0:21:40
 1:10:37
1:10:37
 0:02:11
0:02:11
 0:37:37
0:37:37
 0:04:22
0:04:22
 0:16:21
0:16:21
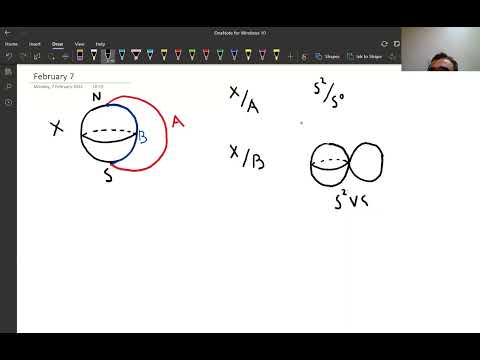 1:34:46
1:34:46
 0:00:55
0:00:55
 0:14:57
0:14:57
 0:54:22
0:54:22
 0:45:22
0:45:22
 0:06:03
0:06:03