filmov
tv
Simplifying Expressions With Roots and Exponents

Показать описание
Now we have all these pesky terms with exponents and roots, and they come in all these complicated looking expressions. Square this, cube root that, whatever will we do? Don't worry, it's usually pretty easy to simplify these until they get into a more palatable form, and it's quite satisfying to get them there! Let's learn all the tricks.
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Simplifying Expressions With Roots and Exponents
Simplifying Radicals Easy Method
How To Simplify Radicals
Simplifying Radicals Easy Method
Simplifying Radicals - Grade 9 Math
Simplifying Radicals with Variables and Exponents
Adding and Subtracting Radical Expressions With Square Roots and Cube Roots
Simplifying radicals simplify a square root expression
Square root #shorts #mathematics #maths #mathstricks #simplification #competativeexams #psc #ssc
Simplifying the cube root of a radical expression
Simplifying Exponents With Fractions, Variables, Negative Exponents, Multiplication & Division, ...
How To Simplify Square Roots
Simplifying the square root of an expression
How to Simplify Radicals (NancyPi)
Simplifying square-root expressions | Mathematics I | High School Math | Khan Academy
Rationalize the Denominator and Simplify With Radicals, Variables, Square Roots, Cube Roots, Algebra
Simplifying Square Roots | Math with Mr. J
08 - Rules to Multiply & Divide Radicals in Algebra (Simplifying Radical Expressions)
Simplifying a radical expression using rational exponents
Simplifying square roots | Exponents, radicals, and scientific notation | Pre-Algebra | Khan Academy
Simplifying the cube root of an algebraic expression
Solving Algebraic Equations With Roots and Exponents
Simplifying Radical Expressions - Laws of Radicals
Math Antic - Simplifying Square Roots
Комментарии
 0:08:23
0:08:23
 0:03:42
0:03:42
 0:13:14
0:13:14
 0:03:06
0:03:06
 0:19:46
0:19:46
 0:03:23
0:03:23
 0:11:20
0:11:20
 0:02:39
0:02:39
 0:00:16
0:00:16
 0:02:13
0:02:13
 0:11:48
0:11:48
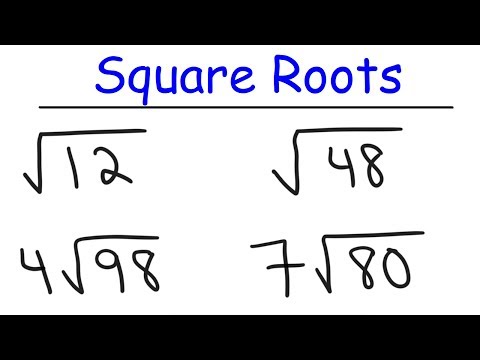 0:10:46
0:10:46
 0:01:28
0:01:28
 0:17:51
0:17:51
 0:08:29
0:08:29
 0:10:55
0:10:55
 0:07:44
0:07:44
 0:29:10
0:29:10
 0:04:26
0:04:26
 0:03:09
0:03:09
 0:02:52
0:02:52
 0:05:46
0:05:46
 0:14:46
0:14:46
 0:12:01
0:12:01