How to Learn General Theory of Relativity | General Relativity | General Relativity Explained

#howtolearngeneraltheoryofrelativity
#generalrelativity
#generalrelativityexplained

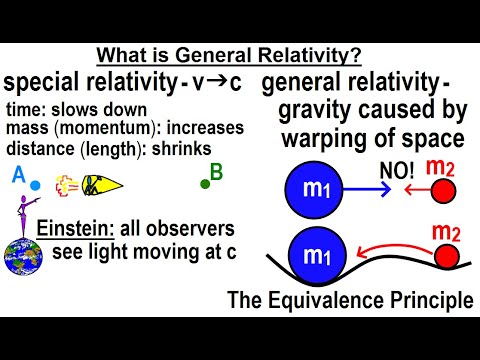
How to learn General Theory of Relativity. In this video, general relativity is explained clearly and simply. This fourth episode of General Relativity explains the role of differential geometry on General Relativity. You will learn in this video, differential geometry plays a very important role in framing the mathematics of General Relativity. Starting from the concepts of curvature, manifolds, metric tensor, this video will give you a complete understanding of the relation between Differential geometry and General Relativity. You will learn the best books to read to learn manifold, an important concept as well as the best books in differential geometry.

00:00 - 01:12 - Introduction
01:13 - 04:49 - A quick recap
04:50 - 06:39 - Flat spacetime and Curved spacetime
06:40 - 09:31 - Geometry of gravity
09:32 - 14:01 - Role of differential geometry in General Relativity
14:02 - 29:25 - Why do we need Differential Geometry
29:26 - 35:44 - Manifolds and General Relativity
35:45 - 37:28 - Why you should learn Manifold
37:29 - 46:53 - Books on Manifold
46:54 - 50:22 - Best online lectures on Manifold
50:23 - 52:48 - Metric Tensor and General Relativity
52:49 - 53:45 - Geodesics and General Relativity
53:46 - 01:05:42 - Best books on Differential Geometry
01:05:43 - 01:06:31 - Conclusion

Subscribe for more physics and mathematics videos:

Join this channel to get access to perks:

Contact: [phone]

The objective of this channel is to provide educative videos on physics and mathematics.

Playlists:

(1) Most watched videos

(2) General Relativity

(3) Special Relativity

(4) Topology

(5) Black Holes

(6) Career In Mathematics

(7) Differential Geometry

(8) Maxwell's Equations

(9) Real Analysis

(10) Vectors and Tensors

(11) Tagore Einstein conversations

(12) History of Science

(13) Concept Building

(14) Classical Physics

(15) Stephen Hawking

(16) Grigori Perelman

(17) Basic Mathematics

(18) Calculus

My name is Shounak. I teach in a college. My subject of specialization is the general theory of relativity, tensor calculus, and topology. I also teach communicative English.

Copyright © 2021 Physics for Students. All rights reserved.

#introductiontogeneralrelativity
#generalrelativityforbeginners
#easyapproachtogeneralrelativity
#generalrelativityexplainedsimplyandvisually
#generalrelativityexplainedfordummies
#howtodtudyrelativity
#howtounderstandrelativity
#howtounderstandgeneralrelativity
#generalrelativitylectureseries
#generalrelativityformathematicians
#generalrelativityfordummies
#einsteinfieldequations
#einsteinfieldequationsexplained
#einsteinfieldequationsforgeneralrelativity
#mathsthatyouneedtoknowtolearngeneralrelativity
#mathematicalprerequisitesforgeneralrelativity
#generalrelativityforstudents
#howtostudygeneralrelativity
#generalrelativitystudyguide
#generalrelativitystepbystep
#physicsforstudents
#generalrelativityintroduction
#generalrelativityforbeginners

[galaxyin]

I picked the post below on quora. Sharing it as an important pedagogical insight on GTR :

There are two basic mathematical approaches to GR. Both rely on differential geometry, which is calculus on arbitrarily curved surfaces, essentially. (The arbitrarily curved surface specific to GR is spacetime itself, which is modelled as a 4-dimensional pseudo-Riemannian manifold, to be exact.)

One approach, (general) tensor calculus, is the older, more 'traditional' way of doing differential geometry and GR, and was the mathematical language that Einstein originally used when developing the theory.

The more modern approach uses all the tools and concepts of modern differential geometry - tangent spaces, the calculus of forms, Lie derivatives, and so on.

Of the two approaches, the notation of tensor calculus looks more fiddly and complicated, but I think it is actually the more 'intuitive' and conceptually simple of the two; it focuses on the physics,  avoids too much conceptual abstraction and requires the least background in related pure mathematics. Perhaps for this reason it is still very popular amongst physicists (if not mathematicians), and the majority of physics research papers still use it (and it also probably helps to ensure the widest possible readership of those papers).

The more modern approach has the advantage that its notation is generally more compact and elegant than tensor notation. However, this notational simplicity actually conceals a good deal of mathematical complexity underneath, and the student is required to become familiar with far more pure mathematics than is required for the tensor approach. But because of its greater mathematical and conceptual sophistication, the modern approach is probably the more powerful of the two approaches overall, and is favoured by many research physicists - and especially mathematicians - for this reason.

My advice would be to learn the tensor approach first, as this will enable you to start learning general relativity sooner, with the minimum of preliminary mathematical study. Once you are comfortable with the tensor approach, learn the modern approach.

On the other hand, if you don't know which approach is best for you, or just want to learn both anyway, you could do a lot worse than reading Gravitation [1], by Misner, Wheeler and Thorne. This hefty, formidable-looking tome is actually very well-written, in a clear and accessible style, and has been rightly regarded as the definitive Bible of General Relativity since it was first published 40 years ago. One big selling-point of the book is that it covers both the tensor and the modern approaches to the subject and uses them in parallel for most of the text, so you can really understand how the two relate to each other, and where one approach might be superior to the other for certain applications.

[ParallaxParadigm]

Sir..what about Gravitation by Misner, Throne and Wheeler..

[m.selvakumarmpcb]

Sir, can you please tell me what are the prerequisites to learn Hilbert spaces

[galaxyin]

If we read a book like schutz ( Introduction to general Relativity). Wouldn't it contain all the mathematics that is needed.

[Ssj-mjic]

Sir if i use tensors and differential geometry by prasoon kumar then can i directly dive into the book general relativity by R Wald??
Is prasoon kumar book sufficient for intermediate understanding of General theory of relativity??

[chung-chiachen]

Sir, it's written torsion free, what's the difference?