filmov
tv
Το Πυθαγόρειο Θεώρημα, στα γρήγορα

Показать описание
Μια γρήγορη παρουσίαση του Πυθαγόρειου Θεωρήματος με τρεις διαφορετικούς οπτικούς τρόπους. Β γυμνασίου και Β λυκείου γεωμετρία.
Το Πυθαγόρειο Θεώρημα, στα γρήγορα
Το πυθαγόρειο θεώρημα //Ορισμός και εφαρμογές //Παραδείγματα...
Τι είναι το Πυθαγόρειο θεώρημα - Μαθηματικά β γυμν
Πυθαγόρειο Θεώρημα
Απόδειξη Πυθαγορείου Θεωρήματος Έξυπνα και Γρήγορα!
Πυθαγόρειο θεώρημα
ΑΠΟΔΕΙΞΕΙΣ ΧΩΡΙΣ ΛΟΓΙΑ,(ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ)
Το αντίστροφο του Πυθαγορείου: πώς αποδεικνύω ότι ένα τρίγωνο είναι ορθογώνιο/ Γεωμετρία Β Γυμνασίου...
ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ
Το Πυθαγόρειο Θεώρημα σε 60 δευτερόλεπτα
Πυθαγόρειο θεώρημα (και μία άλλη απόδειξη)
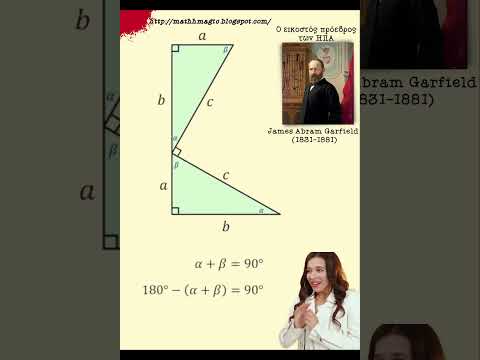
Ποιος Αμερικανός Προέδρος απέδειξε το πυθαγόρειο θεώρημα;...
Πυθαγόρειο Θεώρημα
Πυθαγόρειο Θεώρημα #shorts #maths #μαθηματικα
λυμένες ασκήσεις στο Πυθαγόρειο Θεώρημα
Πυθαγόρειο Θεώρημα | e-du.gr | Περιγραφή και παράδειγμα
Πυθαγόρειο Θεώρημα - Β΄ Γυμνασίου
Επεισόδιο 11 : Η απόδειξη του Einstein για το Πυθαγόρειο Θεώρημα + άλλη μια ! ( γυμνάσιο + λύκειο )...
πυθαγορειο θεωρημα(παραδ8)
ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ
Πυθαγόρειο θεώρημα - PYTHAGOREAN THEOREM
Πυθαγόρειο Θεώρημα (Κατσαρής Ηλίας - ΚΕΔΙΒΙΜ ΠΘ)
Το πυθαγόρειο θεώρημα
ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ (Pythagorean theorem)...
Комментарии
 0:01:48
0:01:48
 0:08:08
0:08:08
 0:06:32
0:06:32
 0:01:18
0:01:18
 0:03:50
0:03:50
 0:04:19
0:04:19
 0:00:58
0:00:58
 0:05:06
0:05:06
 0:01:02
0:01:02
 0:01:01
0:01:01
 0:00:34
0:00:34
 0:01:00
0:01:00
 0:10:21
0:10:21
 0:00:16
0:00:16
 0:03:34
0:03:34
 0:01:50
0:01:50
 0:05:59
0:05:59
 0:13:17
0:13:17
 0:03:06
0:03:06
 0:05:03
0:05:03
 0:05:33
0:05:33
 0:02:46
0:02:46
 0:04:48
0:04:48
 0:24:44
0:24:44