filmov
tv
1 Olympiad Math Q. For Everyone

Показать описание
1 Olympiad Math Q. For Everyone
Class 1 Math Olympiad | Online Quiz | Maths Olympiad Questions for Practice
Math Olympiad Question | You should know this trick!!
Class 1 Math Olympiad Question Paper 2022 23 | Math Olympiad Exam for Class 1| Olympiad Exam Class 1
The unexpectedly hard windmill question (2011 IMO, Q2)
Maths olympiad class 1 | Questions for maths olympiad class 1| Part 1
Math Olympiad question | Trending shorts || #shorts #youtubeshorts #short
Class 1 Math Olympiad Question Paper| Olympiad Exam Class 1| IMO for Class 1|Math Olympiad Exam 2023
A awesome mathematics Exponential problem | Olympiad Question | x^3-1/x^2=?
Basic 2-D Shapes, Class 1, Math Olympiad
A beautiful international math olympiad problem
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Math Olympiad for class 1 & 2 | Online Quiz | Time Questions for Practice for class 1 & 2 | ...
rank 1 in school level in IMO INTERNATIONAL OLYMPIAD EXAM #rank1 #goldmedal #unstoppable
Class 1 Math Olympiad | Online Quiz | Maths Olympiad Questions for Practice | Part 2
New Zealand - Math olympiad Question
Math Olympiad questions | Algebra problems
International Olympiad Exam (IMO) Enters the Chat ☠️ #PW #Shorts #Exams
Norway Math Olympiad Question | You should be able to solve this!
Maths Olympiad question paper 2021-22 Class 1 || Olympiad exam for Class 1|| IMO || Bright Kidzz
Class 1 Math Olympiad | Online Quiz
A Nice Math Olympiad Exponential Equation 3^x = X^9
Math Olympiad Practice
Mental Math 🔥
Комментарии
 0:00:18
0:00:18
 0:12:28
0:12:28
 0:00:33
0:00:33
 0:19:44
0:19:44
 0:16:03
0:16:03
 0:12:55
0:12:55
 0:00:15
0:00:15
 0:18:37
0:18:37
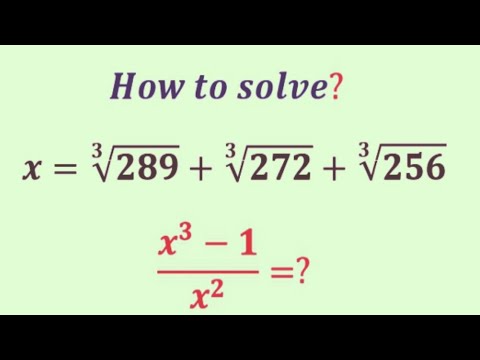 0:11:48
0:11:48
 0:00:19
0:00:19
 0:01:00
0:01:00
 0:00:52
0:00:52
 0:14:18
0:14:18
 0:00:15
0:00:15
 0:14:55
0:14:55
 0:01:12
0:01:12
 0:00:57
0:00:57
 0:00:16
0:00:16
 0:03:21
0:03:21
 0:10:25
0:10:25
 0:06:53
0:06:53
 0:02:34
0:02:34
 0:01:00
0:01:00
 0:00:11
0:00:11