filmov
tv
Which is greater? Ⅰ 95% fail to solve!
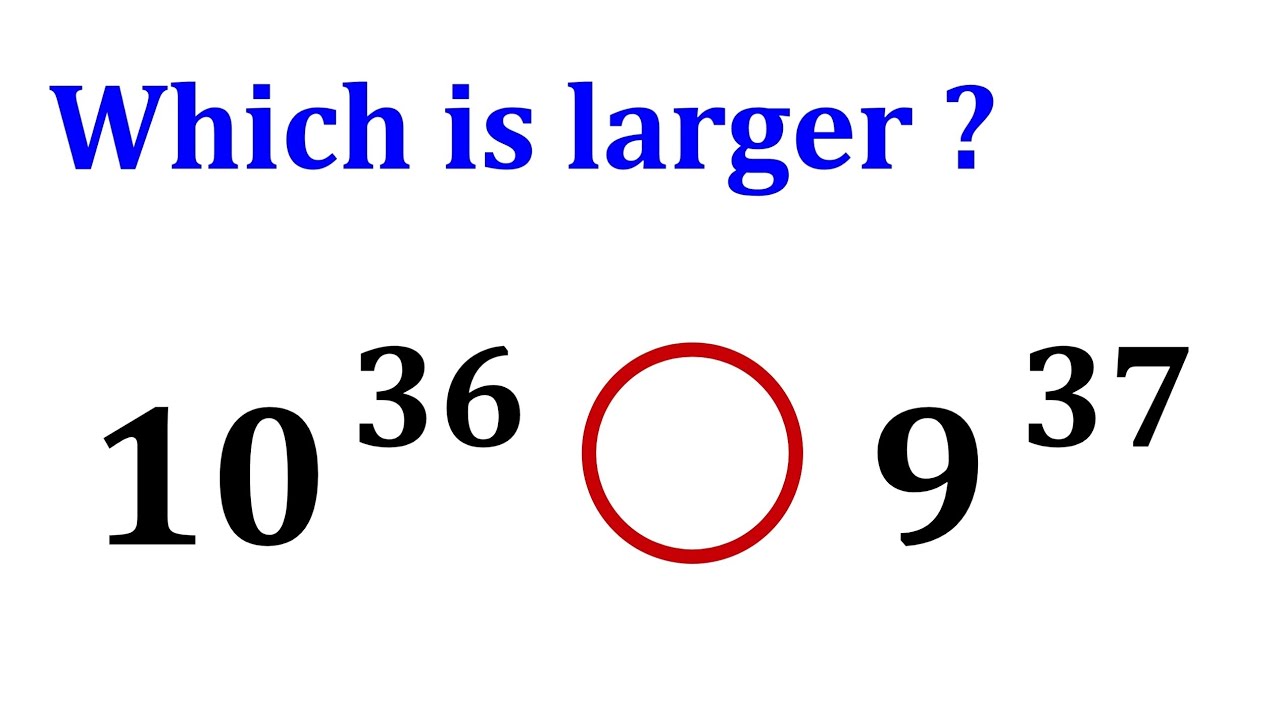
Показать описание
Which is larger, 10^36 or 9^37? How do you solve this equation? Leran the wonderful method.
Which is greater? Ⅰ 95% fail to solve!
XRP TO HIT # 1 Position IN MARCH8-9? A 95% Chance YES! Happy New Year From Mel & Amber ❤️❤️❤️...
Master the Art of Comparing and Ordering Fractions Greater than 1
Apple to pay $95M to settle lawsuit that alleges Siri is spying on its users
Lanes on I-95 reopen after multi-vehicle crash near Timmonsville
Rich Dad Series #95 (Pt.1) - Subscribe for more (official @hubertceo) #shorts!
1 January 2025 | EPS 95 Higher pension latest news today | EPFO pension supreme court live news
5 projects is more fun than 1 🤣
I NEED 1 MORE SUBSCRIBER!!
RODMAN ➡️ PIPPEN. Jordan's greatest teammates. Watch Game 1 vs 2005 Spurs now playing in my cha...
Woman mourns newlywed husband who died on I-95 working as Road Ranger in Hollywood
OMG 1 MORE!!!!!!
Math 95 5 1 The Greatest Common Factor; Factoring by Grouping
female kpop idol who fits more than 95% kbs (pt.1) (no hate) #kpop
Subscribe For More! What Does 1 TBSP Of Peanut Butter Actually Look Like? 🤔 #Shorts
1 Vs 95 The largest number of both😍
Man killed in wrong-way crash on I-95
Interstate 1-95 last night #shorts Subscribe and like for more
Lovely phone cases for iPhone Samsung Huawei and more #phonecase
HANGTIME by Jordan vs Kobe. More highlights from Game 1 of these Finals, up in my channel!
FFRK The Greatest Hunt Banner 1【#95】
Day 1/100 of daily art challenge subscribe for more #drawing #art
2 big air max 95 collabs back to back? more travis 1 lows? + more news
Part 1/2. Start learning Today! Check my channel for more videos.
Комментарии
 0:05:45
0:05:45
 0:07:40
0:07:40
 0:08:14
0:08:14
 0:01:53
0:01:53
 0:00:31
0:00:31
 0:00:40
0:00:40
 0:03:05
0:03:05
 0:00:19
0:00:19
 0:00:50
0:00:50
 0:00:20
0:00:20
 0:02:08
0:02:08
 0:00:06
0:00:06
 0:40:44
0:40:44
 0:00:22
0:00:22
 0:00:23
0:00:23
 0:00:59
0:00:59
 0:00:41
0:00:41
 0:00:16
0:00:16
 0:00:09
0:00:09
 0:00:24
0:00:24
 0:02:08
0:02:08
 0:00:15
0:00:15
 0:21:55
0:21:55
 0:00:15
0:00:15