filmov
tv
10 Limits at Infinity

Показать описание
10 Calculus Limits
Do you have what it takes to calculate 10 limits at infinity? In this video I show you standard technicians for dealing with those limits
Do you have what it takes to calculate 10 limits at infinity? In this video I show you standard technicians for dealing with those limits
How To Find The Limit At Infinity
10 Limits at Infinity
Infinite Limit Shortcut!! (Calculus)
Learn how to evaluate a limit at infinity
This is a very famous limit
Calculus Limits at Infinity The Limit of (x^9 - 1)/(x^(10) + 4) as x approaches infinity
Limits at Infinity & Horizontal Asymptotes
Infinite Limits (Limit Example 10)
Limits Top 10 Must Knows (all of limits in 39 minutes!)
Calculus - HOW TO: Limits at Infinity (Beginner Level)
Limits That Approach Infinity (Calculus)
Limits at Infinity
Solving Limits Mentally #calculus #limit #infinity #rational
Infinite Limits and Vertical Asymptotes
Limits at Infinity of Exponential Functions | How to find limits at infinity | Calculus - Part 4
Delta-Epsilon proof of Infinite limit
Limits at Infinity & Infinite Limits | jensenmath.ca
Limits and Infinity / Calculus / Interactive Video
Limit of arctan function as x approaches infinity [Limits at infinity]
Lecture#10 Limit at Infinity
(New Version Available) Limits At Infinity
Evaluating Limits at Infinity - Problem 10 - Limits - Diploma Engineering Mathematics 2
Find Asymptote for the Rational Function Use Limits at Infinity Calculus Q10 Solution
Evaluating Limits from a Graph
Комментарии
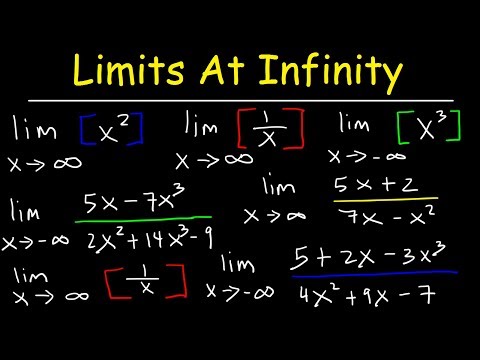 0:13:14
0:13:14
 0:30:55
0:30:55
 0:00:51
0:00:51
 0:01:40
0:01:40
 0:00:48
0:00:48
 0:02:01
0:02:01
 0:19:24
0:19:24
 0:05:11
0:05:11
 0:39:46
0:39:46
 0:19:57
0:19:57
 0:00:59
0:00:59
 0:09:54
0:09:54
 0:01:00
0:01:00
 0:29:04
0:29:04
 0:16:35
0:16:35
 0:09:26
0:09:26
 0:14:40
0:14:40
 0:12:45
0:12:45
 0:07:09
0:07:09
 0:10:23
0:10:23
 0:09:42
0:09:42
 0:08:39
0:08:39
 0:06:57
0:06:57
 0:00:46
0:00:46