filmov
tv
Aliasing and the Sampling Theorem Simplified

Показать описание
A presentation of aliasing, the sampling theorem, and the Fourier transform representation of a sampled signal that does not make extensive use of Fourier transform properties and impulse trains, but instead relies on the relationship between continuous- and discrete-time frequency and the non uniqueness of discrete-time sinusoids.
What is aliasing and the Nyquist theorem?
Sampling, Aliasing & Nyquist Theorem
The intuition behind the Nyquist-Shannon Sampling Theorem
Aliasing explained #VeritasiumContest
Aliasing and the Sampling Theorem
Sampling Theory and Aliasing | Image Processing II
Aliasing and the Sampling Theorem Simplified
Aliasing & Sampling Theorem | Digital Signal Processor
Aliasing and Nyquist - Introduction & Examples
Shannon Nyquist Sampling Theorem
Nyquist Shannon Sampling Theorem
How to Understand Aliasing in Digital Sampling ('Best explanation ever!!!')
Sampling Theory and Aliasing
2. Sampling Theorem - Digital Audio Fundamentals
Sampling Theorem
Aliasing or Effect of Under Sampling | Generation of Aliasing | Effect and Solution of Aliasing
What is Aliasing #shorts
What is The Nyquist Rate?
Aliasing Error | Sampling Theorem | Signals and Systems
Aliasing #sampling #nyquist #python #signalprocessing #github
Sampling Theorem: Derivation Part 2
Sampling Theorem and Aliasing
LECT-25: Sampling , Aliasing & Nyquist Rate
Electronics 18: Sampling, Nyquist, Aliasing, Analog to Digital (ADC) and Digital to Analog (DAC)
Комментарии
 0:03:29
0:03:29
 0:10:47
0:10:47
 0:11:25
0:11:25
 0:01:01
0:01:01
 0:14:25
0:14:25
 0:12:08
0:12:08
 0:19:19
0:19:19
 0:14:05
0:14:05
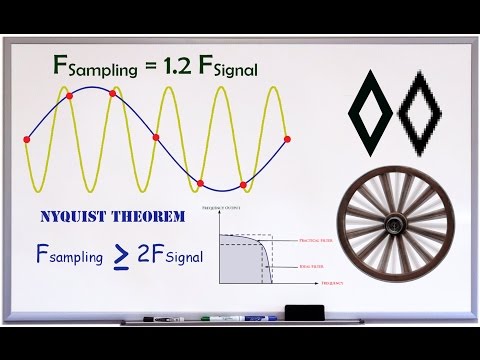 0:02:18
0:02:18
 0:17:19
0:17:19
 0:02:55
0:02:55
 0:05:10
0:05:10
 0:40:32
0:40:32
 0:20:40
0:20:40
 0:20:35
0:20:35
 0:07:12
0:07:12
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:06:58
0:06:58
 0:00:26
0:00:26
 0:10:45
0:10:45
 0:24:42
0:24:42
 0:18:57
0:18:57
 0:36:05
0:36:05