filmov
tv
Integral of sqrt(25-4x^2) trig substitution integral.

Показать описание
In this classic trig substitution problem, we find the indefinite integral of sqrt(25-4x^2). We plan to exploit the trig identity cos^2(theta)=1-sin^2(theta) because the inside of the square root has the form "constant-variable^2".
We cleverly pick the substitution x=5/2sin(theta), which will cancel the factor of 4 and leave us with a 25 to factor out of the square root. We also have to transform the differential dx=5/2cos(theta)d(theta), and the integral reduces to the integral of cosine squared.
We handle the trigonometric integral cos^2(x) by applying the power reducing identity cos^2(x)=1/2*(1+cos(2x)) and complete the integral by guessing the antiderivative of each term. But we aren't done yet!
We still have to transform the antiderivative in terms of x, so we go back to the original trig substitution and solve for theta. Subbing in theta = arcsin(2x/5), we are able to express the answer in terms of x, but there's a lingering problem: we have the cosine of twice the inverse sine of 2x/5!
To make progress, we use the identity sin(2theta)=2sin(theta)cos(theta). Now the last remaining problem is to evaluate cos(arcsin(2x/5)), which we do using a geometric construction (we find a trig function of an inverse trig function by using a right triangle).
We clean up a few constants, and we're done with the trig substitution integral!
We cleverly pick the substitution x=5/2sin(theta), which will cancel the factor of 4 and leave us with a 25 to factor out of the square root. We also have to transform the differential dx=5/2cos(theta)d(theta), and the integral reduces to the integral of cosine squared.
We handle the trigonometric integral cos^2(x) by applying the power reducing identity cos^2(x)=1/2*(1+cos(2x)) and complete the integral by guessing the antiderivative of each term. But we aren't done yet!
We still have to transform the antiderivative in terms of x, so we go back to the original trig substitution and solve for theta. Subbing in theta = arcsin(2x/5), we are able to express the answer in terms of x, but there's a lingering problem: we have the cosine of twice the inverse sine of 2x/5!
To make progress, we use the identity sin(2theta)=2sin(theta)cos(theta). Now the last remaining problem is to evaluate cos(arcsin(2x/5)), which we do using a geometric construction (we find a trig function of an inverse trig function by using a right triangle).
We clean up a few constants, and we're done with the trig substitution integral!
 0:08:53
0:08:53
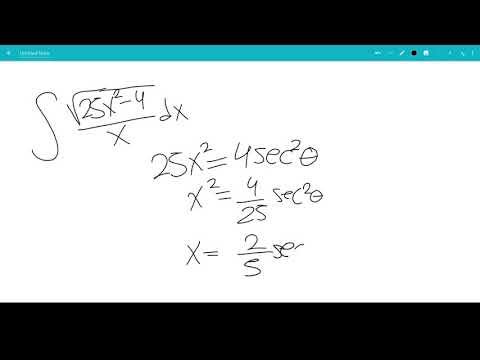 0:04:17
0:04:17
 0:08:36
0:08:36
 0:08:45
0:08:45
 0:19:03
0:19:03
 0:04:38
0:04:38
 0:07:22
0:07:22
 0:09:20
0:09:20
 0:08:31
0:08:31
 0:03:04
0:03:04
 0:06:27
0:06:27
 0:26:06
0:26:06
 0:07:49
0:07:49
 0:38:08
0:38:08
 0:06:32
0:06:32
 0:06:37
0:06:37
 0:03:38
0:03:38
 0:09:57
0:09:57
 0:03:36
0:03:36
 0:03:37
0:03:37
 0:10:37
0:10:37
 0:04:10
0:04:10
 0:00:11
0:00:11
 0:12:27
0:12:27