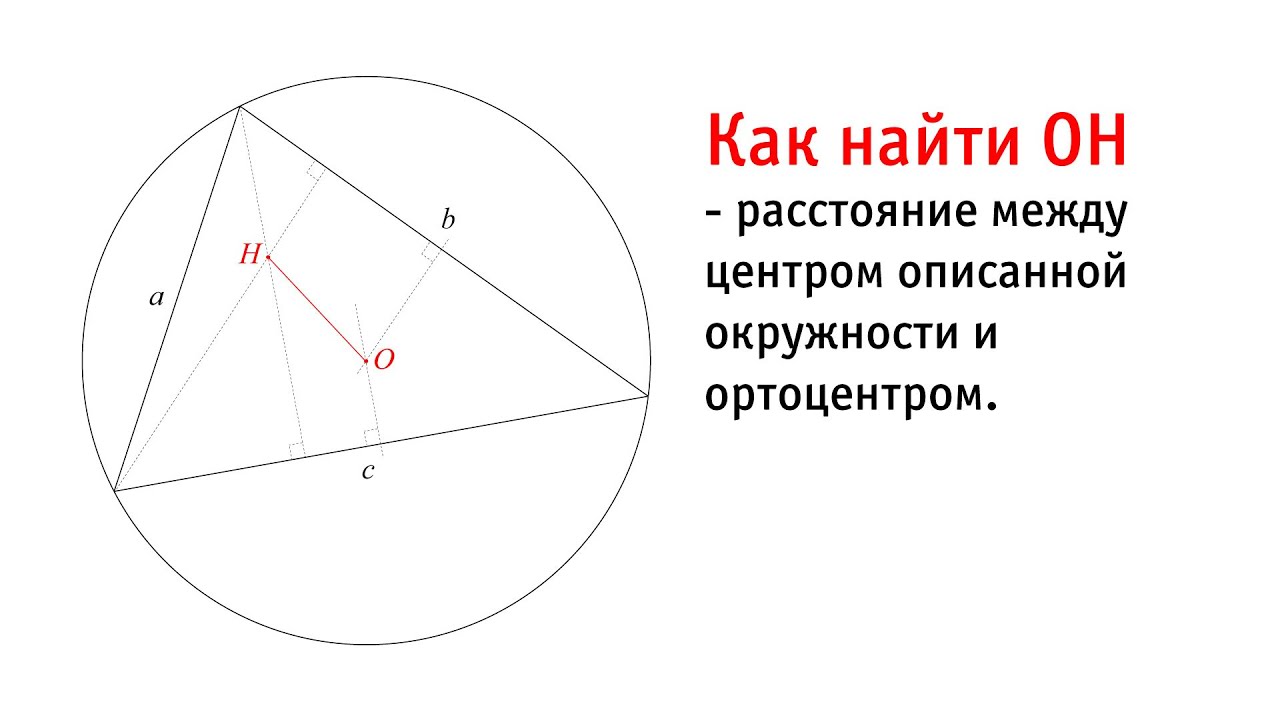
Найти расстояние от центра описанной около треугольника окружности до его ортоцентра

В сегодняшней задаче будет найдено расстояние от центра описанной около треугольника окружности до его ортоцентра.
Будет рассмотрено два способа решения. Первый можно назвать традиционным, и он основан на теореме косинусов. Второй способ потребует привлечения более мощного, однако все же школьного аппарата.

Читает Игорь Тиняков для канала Элементарная Математика

#ортоцентр #центрописаннойокружности #окружностьэйлера

[ЧВА-оо]

Игорь Геннадьевич! Ваш канал самый лучший в РФ!!!

[vacman]

Очень, очень хорошее и сильное видео. Знал эту конструкцию полностью, но все равно открыл для себя новые способы доказательств старых фактов, спасибо большое за ваш огромный труд!

[olialderson]

спасибо, ждём продолжения лекций по теорверу)

[vladyatsuk]

Спасибо за видео, правда пока еще не посмотрел полностью.
20:45 отсюда интересный результат, что произведение косинусов углов треугольника не больше 1/8 :)
А есть или будет видео про формулу Карно? В книге для остроугольного треугольника увидел доказательство с помощью теоремы Птолемея, знаю, что еще можно решить с помощью cosa+cob+cosc=1+r/R (и отсюда неравенство cosa+cob+cosc <= 3/2)
И еще хотелось бы увидеть видео равенствами/неравенствами с элементами треугольника ( с тригонометрией, как в примере выше, или например что-то типа h1+h2+h3>=9r) Еще раз спасибо за Вашу работу!

[karowhiteblackhouse]

Игорь, день добрый. А задачу Мишустина вторым способом решить возможно? Первый способ есть на ютубе.