Integral of (2x+7)/(4+(1+x)^2) (substitution)

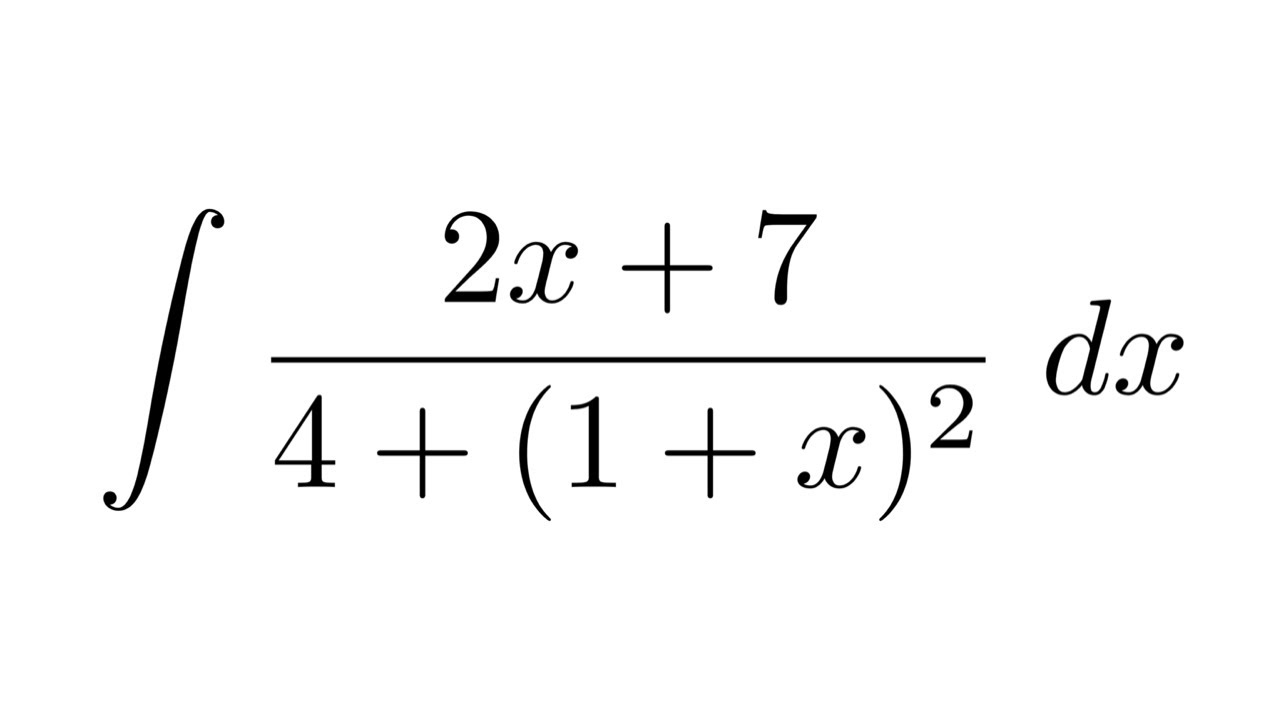
Показать описание

👋 𝐅𝐨𝐥𝐥𝐨𝐰 @𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥𝐬𝐟𝐨𝐫𝐲𝐨𝐮 𝐟𝐨𝐫 𝐚 𝐝𝐚𝐢𝐥𝐲 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥 😉

🚶 𝐒𝐭𝐞𝐩𝐬
00:00 Write 7 as 2+5
00:17 Split into two integrals
00:49 Rewrite expression
02:03 Substitution: u=x^2+2x+5
02:20 Differentiate in both sides
02:27 Substitution: v=(1+x)/2
02:35 Differentiate in both sides
02:46 Substitute x^2+2x+5 and (2x+2)dx
03:01 Substitute (1+x)/2 and dx
03:24 Integrate 1/u
03:28 Simplify and integrate 1/(1+v^2)
03:42 Undo substitution: u in terms of x
03:51 Undo substitution: v in terms of x
04:01 Add integration constant +C
04:11 Final answer!
04:15 See more!

𝐈𝐧𝐭𝐞𝐠𝐫𝐚𝐭𝐢𝐨𝐧 𝐦𝐞𝐭𝐡𝐨𝐝𝐬 𝐩𝐥𝐚𝐲𝐥𝐢𝐬𝐭𝐬

🎓 𝐇𝐚𝐯𝐞 𝐲𝐨𝐮 𝐣𝐮𝐬𝐭 𝐥𝐞𝐚𝐫𝐧𝐞𝐝 𝐚𝐧 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐭𝐢𝐨𝐧 𝐦𝐞𝐭𝐡𝐨𝐝? 𝐅𝐢𝐧𝐝 𝐞𝐱𝐚𝐦𝐩𝐥𝐞𝐬 𝐨𝐟 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥𝐬 𝐬𝐨𝐫𝐭𝐞𝐝 𝐛𝐲 𝐥𝐞𝐯𝐞𝐥 (𝐞𝐚𝐬𝐲, 𝐦𝐞𝐝𝐢𝐮𝐦 𝐚𝐧𝐝 𝐡𝐢𝐠𝐡) 𝐢𝐧 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥𝐬𝐟𝐨𝐫𝐲𝐨𝐮.𝐜𝐨𝐦:

𝐅𝐨𝐥𝐥𝐨𝐰 𝐈𝐧𝐭𝐞𝐠𝐫𝐚𝐥𝐬 𝐅𝐨𝐫𝐘𝐨𝐮

𝐇𝐨𝐰 𝐭𝐨 𝐝𝐨𝐧𝐚𝐭𝐞

#integralsforyou #integrals #integration

Рекомендации по теме

Комментарии

🔍 𝐀𝐫𝐞 𝐲𝐨𝐮 𝐥𝐨𝐨𝐤𝐢𝐧𝐠 𝐟𝐨𝐫 𝐚 𝐩𝐚𝐫𝐭𝐢𝐜𝐮𝐥𝐚𝐫 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥? 𝐅𝐢𝐧𝐝 𝐢𝐭 𝐰𝐢𝐭𝐡 𝐭𝐡𝐞 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥 𝐬𝐞𝐚𝐫𝐜𝐡𝐞𝐫:

🎓 𝐇𝐚𝐯𝐞 𝐲𝐨𝐮 𝐣𝐮𝐬𝐭 𝐥𝐞𝐚𝐫𝐧𝐞𝐝 𝐚𝐧 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐭𝐢𝐨𝐧 𝐦𝐞𝐭𝐡𝐨𝐝? 𝐅𝐢𝐧𝐝 𝐞𝐚𝐬𝐲, 𝐦𝐞𝐝𝐢𝐮𝐦 𝐚𝐧𝐝 𝐡𝐢𝐠𝐡 𝐥𝐞𝐯𝐞𝐥 𝐞𝐱𝐚𝐦𝐩𝐥𝐞𝐬 𝐡𝐞𝐫𝐞:

👋 𝐅𝐨𝐥𝐥𝐨𝐰 @𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥𝐬𝐟𝐨𝐫𝐲𝐨𝐮 𝐟𝐨𝐫 𝐚 𝐝𝐚𝐢𝐥𝐲 𝐢𝐧𝐭𝐞𝐠𝐫𝐚𝐥! 😉

🙋‍♂ 𝐃𝐨𝐧𝐚𝐭𝐞:

IntegralsForYou

Here's how I solved it:

integral of 2x+7/4+(1+x)^2dx
= integral of 2x+2+5/4+(1+x)^2dx
= integral of 2x+2/4+(1+x)^2dx + integral of 5/4+(1+x)^2dx

Then I applied two u-subs:

For the integral of 2x+2/4+(1+x)^2dx
u=1+x
du=1dx
x = u-1

For the integral of 5/4+(1+x)^2dx
u=1+x
du=1dx

Therefore:

integral of 2(u-1)+2/4+u^2du + integral of 5/4+u^2du
So: integral of 2u-2+2/4+u^2du + integral of 5/4+u^2du
Thus I got: integral of 2u/4+u^2du + integral of 5/4+u^2du

I applied another substitution and used the z variable:

So z=4+u^2
dz=2udu

Thus:

integral of 2u/z*(dz/2u) + 5*integral of 1/4+u^2du

After integration of first integrand:

In[4+(1+x)^2] + 5*integral of 1/4(1+u^2/4)du

For second integral:

z=u/2 dz=1/2du
2dz=1du
So: 1/4*integral of 1/1+z^2*(dz/2)
1/2*integral of 1/1+z^2dz
1/2arctan(z) + C
1/2arctan(u/2) + C
1/2arctan(x+1/2) + C

Therefore, the final answer was:

In[4+(1+x)^2] + 5/2arctan(x+1/2) + C

Great video BTW!

erikusmetallicus

That was easy! Btw where are you from?

ayeshamahvish

bukur....if you remember what this is 😂

ansumanc

Integral of (2x+7)/(4+(1+x)^2) (substitution)

Integral of (2x+7)/(4+(1+x)^2) (substitution)

How REAL Men Integrate Functions

Integration By Substitution Problem#2. ∫ (x³+2x)⁵ (6x²+4) dx

Integration By Partial Fractions

How To Integrate Using U-Substitution

What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2

Integration of Rational Functions By Completing The Square - Calculus

Integral of (2x+3)^4 using 'Integration by Substitution' - Complete Walkthrough

Ramblings from Calculus 1 before Exam 3 (Fall 2024)

Integral by completing the square, and u sub, calculus 2

Integration of Rational Functions into Logarithms By Substitution & Long Division

Integrating Exponential Functions By Substitution - Antiderivatives - Calculus

Evaluate the integral by making the given substitution. (Use C) x3(7 + x4)6 dx, u = 7 + x4

How to Integrate Using U-Substitution (NancyPi)

Integration of 1/(2x+7) | Integration by Substitution

5 simple unsolvable equations

Integral with u substitution 7x/(2 - x^2)^3

∫ Integration by Substitution problem #7 ! ! ! ! !

100 integrals (world record?)

Use substitution to evaluate the indefinite integral tan^7 x/2 sec^2 x/2 dx

JEE Aspirants ka Sach 💔 #JEE #JEEMain #Shorts

WHY I HATE MATH 😭 #Shorts

Integration of (7x-2)√(3x+2) dx using Substitution Method By TAZER

Integral of (2x-3)/(2x^2-6x+5) (substitution)