filmov
tv
Calculus 3: Lecture 11.5 Lines and Planes in Space

Показать описание
Calculus 3 Lecture 11.5: Lines and Planes in 3-D
Calculus 3: Lecture 11.5 Lines and Planes in Space
Calculus 3: Vector Calculus in 3-D (9 of 35) How to Determine if the Lines Intersect,
Calculus 3: Line Integrals (26 of 44) Vector Field: Evaluate a Line Integral
Calculus 3: Line Integrals (4 of 44) What is a Line Integral? NOT TO BE CONFUSED WITH
Calculus 3: Line Integrals (27 of 44) Vector Field: Evaluate a Line Integral
Calculus 3: Equations of Lines and Planes (Video #5) | Math with Professor V
Calculus 3: Line Integrals (13 of 44) What is a Line Integral? Find the Center of Mass
calculus | review | limits
Calculus 3: Vector Calculus in 3-D (8 of 35) How to Determine if the Lines are Parallel?
Calculus 3: Vector Calculus in 3-D (6 of 35) Parametric Equations and Vectors: Example 1
Calculus 3: Line Integrals (9 of 44) What is a Line Integral? A Conceptual View
Calculus 3: Line Integrals (19 of 44) Vector Field: Find the Work Done: F(x,y)=(x^2)i-(xy)j Ex. 1
Calculus 3 - Intro To Vectors
Calculus 3: Line Integrals (11 of 44) What is a Line Integral? Example 2.5
ALL of calculus 3 in 8 minutes.
Calculus 3: Vector Calculus in 3-D (16 of 35) Find the Distance Between a Point and a Line
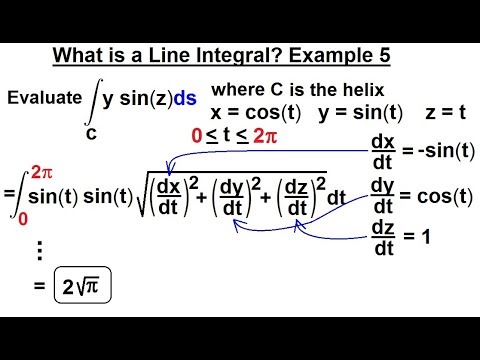
Calculus 3: Line Integrals (17 of 44) What is a Line Integral? [y(sinz)]ds Example 5
Calculus 3: Finding Equations of Lines, Planes & Distances in 3-Space | Math with Professor V
Calculus 3: Ch 2.1 Lines and Vectors in 3-D (11 of 20) Are the 2 Lines Parallel?
Calculus 3: Integration - Equations of Lines & Planes (5 of 27) Find the Symmetric Eqns. of a Li...
Calculus 3: Functions of Several Variables (Video #11) | Math with Professor V
Calculus 3: Integration - Equations of Lines & Planes (8 of 27) Determine If the Lines Intersect
Calculus 3: Line Integrals (29 of 44) What is the Fundamental Theorem for Line Integrals?
Комментарии
 3:21:03
3:21:03
 1:56:40
1:56:40
 0:07:21
0:07:21
 0:04:21
0:04:21
 0:02:13
0:02:13
 0:06:05
0:06:05
 0:47:57
0:47:57
 0:09:04
0:09:04
 1:00:06
1:00:06
 0:02:49
0:02:49
 0:02:58
0:02:58
 0:04:13
0:04:13
 0:08:41
0:08:41
 0:57:54
0:57:54
 0:07:26
0:07:26
 0:08:10
0:08:10
 0:07:28
0:07:28
 0:05:51
0:05:51
 1:20:19
1:20:19
 0:03:53
0:03:53
 0:05:02
0:05:02
 0:34:03
0:34:03
 0:02:59
0:02:59
 0:06:22
0:06:22