filmov
tv
The Degree of a Splitting Field (Algebra 3: Lecture 12 Video 1)

Показать описание
Lecture 12: In this lecture we focused on splitting fields. We first recalled Theorem 25 in Section 13.4, which we proved in an earlier lecture. We proved that if f(x) in F[x] is a polynomial of degree n then the degree of a splitting field K of f(x) over F is at most n!. We discussed a stronger result, that the degree divides n!. We then gave several examples of splitting fields, including the splitting fields of x^3-2, and more generally x^p-2 where p is a prime. We discussed the nth cyclotomic field, which is a splitting field for x^n-1. We showed that x^4-2 and x^4+2 have the same splitting field. At the end of the lecture we defined what it means for a field to be an algebraic closure of F and what it means for a field to be algebraically closed.
Reading: In this lecture we covered much of Section 13.4 of Dummit and Foote, starting on page 537. We have not yet discussed Theorem 27 (but we did state Corollary 28). We gave some of the definitions on page 543, but have not yet discussed Proposition 29. We also mentioned a few Algebra Comprehensive Exam Problems: Fall 2011 #8, Spring 2013 #9, and Fall 2020 #7.
Reading: In this lecture we covered much of Section 13.4 of Dummit and Foote, starting on page 537. We have not yet discussed Theorem 27 (but we did state Corollary 28). We gave some of the definitions on page 543, but have not yet discussed Proposition 29. We also mentioned a few Algebra Comprehensive Exam Problems: Fall 2011 #8, Spring 2013 #9, and Fall 2020 #7.
Find the degree of the splitting field of x^4+2
Find the degree of the splitting field of x^4-2
The Degree of a Splitting Field (Algebra 3: Lecture 12 Video 1)
Splitting Fields of Cubics
LECTURE - 3, ADVANCED ABSTRACT ALGEBRA - II, EXAMPLES OF DEGREE OF SPLITTING FIELD.
Splitting Field , definition , Find degree of splitting field ( Algebra) Lect : 01
Polynomials: Finding the Splitting Field by Finding the Roots
Splitting Field , definition , Find degree of splitting field Lect : 03// (find degree of x^6+1 )
Splitting field of x^4+x^2+1
Prove that the degree of splitting field of x^p-1 is p-1 ,if p is a prime | Splitting field | MSc
Splitting Fields of Polynomials over Finite Fields (Algebra 3: Lecture 23 Video 1)
Examples of Splitting Fields I (Algebra 3: Lecture 12 Video 2)
Splitting field of x^6+1
Splitting field of x^7-7
Splitting Field || Definition || Examples || Field Extension By MATH POINT ACADEMY
Galois theory: Splitting fields
FLOW The Splitting Field of a Polynomial
Splitting Field , definition , Find degree of splitting field ( Algebra) Lect : 02
How to find splitting field,dimension & basis of splitting field (part-2)
Field Extension & Splitting Field Examples | Adjoin Roots: ℚ(√2), ℚ(√3), ℚ(√2,√3)=ℚ(√2)(√3)...
Splitting field of x^3-1 over Q
Splitting Fields Part 1
Splitting field of x^3+x^2+x+1
Examples of Splitting Fields II (Algebra 3: Lecture 12 Video 3)
Комментарии
 0:07:01
0:07:01
 0:06:15
0:06:15
 0:13:47
0:13:47
 0:06:43
0:06:43
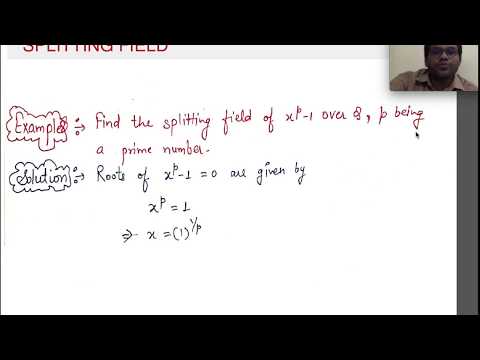 0:10:50
0:10:50
 0:13:05
0:13:05
 0:04:02
0:04:02
 0:14:12
0:14:12
 0:06:38
0:06:38
 0:03:15
0:03:15
 0:22:32
0:22:32
 0:09:51
0:09:51
 0:07:01
0:07:01
 0:15:16
0:15:16
 0:12:28
0:12:28
 0:23:40
0:23:40
 0:19:35
0:19:35
 0:19:17
0:19:17
 0:06:57
0:06:57
 0:29:44
0:29:44
 0:02:55
0:02:55
 0:17:27
0:17:27
 0:02:05
0:02:05
 0:22:31
0:22:31