filmov
tv
Find Exact Value of Cos(2x) & Sin(2x) Given Sin(x)=-Sqrt(3)/5, Cos(x) is + (Double Angle Identities)

Показать описание
Find cos(2x) and sin(2x), given sin(x)=-sqrt(3)/5 and cos(x) is greater than zero. (a) As there are three version for the identity for cos(2x), the version chosen is the one that only contains the given information of sin(x). The value for sin(x) is substituted into cos(2x)=1-2sin^2(x) and the answer is simplified. (b) As sin(2x)=2sin(x)cos(x), the value of cos(x) needed to be found and the method chosen used the Pythagorean Identity sin^2(x)+cos^2(x)=1. It was given that the cos(x) was greater than zero so the positive square root was used when finding cos(x). Finally the values for sin(x) and cos(x) were substituted into the identity for the sin(2x).
Timestamps
0:00 Introduction
0:52 Double Angle Identity for cos(2A)
1:38 Find cos(2x)
3:46 Double Angle Identity for sin(2A)
4:07 Find cos(x)
6:36 Find sin(2x)
Timestamps
0:00 Introduction
0:52 Double Angle Identity for cos(2A)
1:38 Find cos(2x)
3:46 Double Angle Identity for sin(2A)
4:07 Find cos(x)
6:36 Find sin(2x)
How To Find The Exact Values of Trig Functions
Trig: Finding the exact value of cos (2 inv sin 3/5)
Find the Exact Value of cos^2(pi/8) - 1/2
Find Exact Value of Cos(2x) & Sin(2x) Given Sin(x)=-Sqrt(3)/5, Cos(x) is + (Double Angle Identit...
Find exact value for cos^2(1/2 sin^(-1) (3/5)). Half Angle Formula
How To Use a Calculator To Calculate The Exact Value of Cos Pi over 3 | tan(pi/3)
Find Exact Value of Cos^2(pi/8)
EXACT Value Of cos(2x) & sin(2x) From cos(x) = -2/3
SNAP SLOT 1 SHIFT 2 ALL QUANTS QUESTIONS || 8 DECEMBER - OFFICIAL QUESTIONS
Find values of sin 2x, cos 2x, tan 2x when cos x = 2/(sqrt(5)) in quadrant 4. Double Angle Formula
How To Use Reference Angles to Evaluate Trigonometric Functions
Find exact value for cos(2 tan^(-1)(-4/3)). Double Angle Formula
EXACT Values Of cos(2x) & sin(2x) For sin(x) = 7/25 & x In Quadrant 1
Calculate sin2x cos2x and tan2x for given tanx in Quadrant 2
Exact Trig Values - Hand Trick | Trigonometry | Maths | FuseSchool
Find exact value sin(sin^(-1)(1/2)- cos^(-1)(0)). Sum and Difference Formula
Find exact value for cos(2 cos^(-1) 4/5). Double Angle Formula
Evaluating Inverse Trigonometric Functions
Find exact value for cos(2sin^(-1) 3/5). Double Angle Formula
EXACT Value Of cos(x) If cos(2x) = 8/17 & Angle 2x Lies In Quadrant 4
Find Exact Value of cos 11 pi by 12 Compound Angle Formula Trigonometry
MATH 1316 Section 5.5: Solving for cos2x and sin2x values using double angle identities
Trigonometry - Find the exact value of sin cos and tan
cos pi/3 + sin pi/2 find the exact value
Комментарии
 0:12:39
0:12:39
 0:02:57
0:02:57
 0:02:57
0:02:57
 0:08:01
0:08:01
 0:03:13
0:03:13
 0:00:24
0:00:24
 0:06:39
0:06:39
 0:08:39
0:08:39
 1:17:17
1:17:17
 0:03:51
0:03:51
 0:10:59
0:10:59
 0:03:14
0:03:14
 0:08:03
0:08:03
 0:04:07
0:04:07
 0:04:08
0:04:08
 0:02:56
0:02:56
 0:02:19
0:02:19
 0:22:47
0:22:47
 0:02:10
0:02:10
 0:06:56
0:06:56
 0:05:13
0:05:13
 0:09:57
0:09:57
 0:02:48
0:02:48
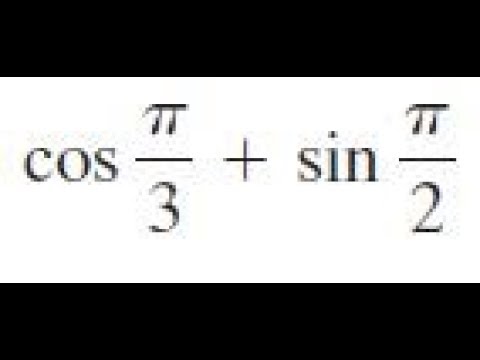 0:00:25
0:00:25