Modular Arithmetic: In Motion

preview_player
Показать описание
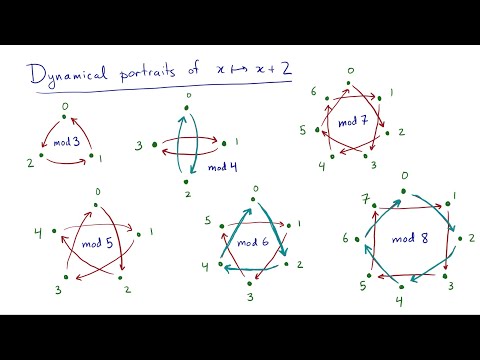
Modular arithmetic visually! We use a visualization tool called a "dynamical portrait." We explore addition and multiplication modulo n, and discover and prove the portrait is made of cycles if and only if the function (f(z) = z+a mod n or f(z) = az mod n) is bijective.

This treatment is inspired by Martin H. Weissman's beautiful book, An Illustrated Theory of Numbers.

This video is appropriate for an introduction to proof course, for undergraduate mathematics majors, or for the mathematically inclined, especially those interested in cryptography or number theory.

For associated materials:
  1. Proof of Concept
  2. modular arithmetic
  3. dynamical portrait
  4. cryptography
  5. discrete mathematics
  6. number theory
Рекомендации по теме
Modular Arithmetic: In 0:18:48

Modular Arithmetic: In Motion

Modular Arithmetic: Addition 0:14:48

Modular Arithmetic: Addition in Motion

Modular Arithmetic: Multiplication 0:23:15

Modular Arithmetic: Multiplication in Motion

This completely changed 0:20:33

This completely changed the way I see numbers | Modular Arithmetic Visually Explained

Mod By A 0:15:25

Mod By A Group: Generalized Modular Arithmetic, from Basic Modular Arithmetic Congruence to 'No...

Modular Arithmetic Multiplication 0:03:58

Modular Arithmetic Multiplication (synthwave)

Modular arithmetic 0:13:25

Modular arithmetic

The Unusual Mathematics 0:14:51

The Unusual Mathematics of Modular Division

Modular Arithmetic 0:00:18

Modular Arithmetic

Modular arithmetic example 0:01:54

Modular arithmetic example (useful for understanding RSA)

Modular Arithmetic 0:20:23

Modular Arithmetic

Why greatest Mathematicians 0:00:38

Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths

That's Why Mohit 0:00:19

That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...

Modular Arithmetic Part 0:03:55

Modular Arithmetic Part 1

Using Modular Arithmetic 0:13:17

Using Modular Arithmetic - Learn These Tricks

Modular Arithmetic: Under 0:17:27

Modular Arithmetic: Under the Hood

Modulo explained for 0:04:06

Modulo explained for motion designers, quickly | Quick After Effects Tip

L58: modular arithmetic 0:38:23

L58: modular arithmetic

Modular Arithmetic - 0:22:40

Modular Arithmetic - Congruence and its Properties - Cryptography - Cybersecurity - CSE4003

Modular arithmetic 0:38:24

Modular arithmetic

Modular Arithmetic & 0:28:09

Modular Arithmetic & Modulus Function (Part 4 Crashcourse Cryptography)

Modular Arithmetic: User's 0:09:23

Modular Arithmetic: User's Manual

MODULAR ARITHMETIC 2 0:07:16

MODULAR ARITHMETIC 2

Modular Arithmetic Part 0:01:26

Modular Arithmetic Part 1 : Questions, questions and questions .

Комментарии
Автор

I've never thought modular arithmetic in a graph form. Beautiful. Alwo thanks for clean representation.

XahhaTheCrimson
Автор

Thanks for the video! l really enjoyed seeing connections to graph theory.. taking abstract algebra and graph theory right now and this visualization helped:) Also the interactive modular dynamics activity on your site! amazing

jessiemeanwell
Автор

Really nice! I teach an Algebra in Argentina. I´ll try to incorporate some of the visuals. I think students are gonna like it!

TheSanmanju