Superposition Principle with Undetermined Coefficients to Solve Non-Homogeneous DEs| Lesson25

Superposition Principle with Undetermined Coefficients to Solve Non-Homogeneous Differential Equations -(I)

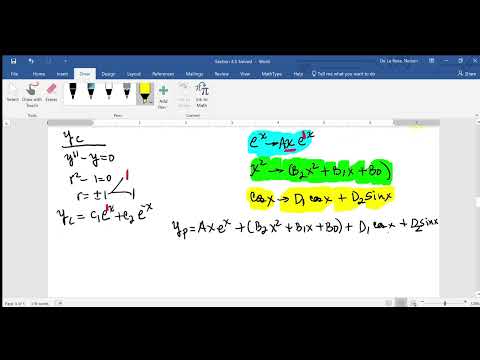
In the context of solving non-homogeneous differential equations, the superposition principle is used to find the particular solution by adding together the solutions to homogeneous and non-homogeneous parts of the equation.

The method of undetermined coefficients involves finding a particular solution to the non-homogeneous differential equation by guessing a form for the solution and then using the method of substitution to find the unknown coefficients. This method can be used in combination with the superposition principle to solve non-homogeneous differential equations.
A question is solved in this video.

Here is a general outline of how to solve a non-homogeneous differential equation using the superposition principle and the method of undetermined coefficients:

Find the general solution to the corresponding homogeneous equation by using characteristic equations or by using the methods of undetermined coefficients or variation of parameters.

Guess a form for the particular solution that matches the form of the non-homogeneous term. Substitute the guess into the non-homogeneous differential equation and solve for the unknown coefficients. Add the general solution to the homogeneous equation and the particular solution to obtain the complete solution to the non-homogeneous equation.

It is important to note that the choice of form for the particular solution will depend on the form of the non-homogeneous term. In some cases, it may be necessary to guess multiple forms for the particular solution and then add them together to find the complete solution.

THE BEST THING TO DO ON THIS CHANNEL IS TO LIKE, SUBSCRIBE/COMMENT AND SHARE THE VIDEOS . THIS IS REALLY APPRECIATED