filmov
tv
Integral of x*sinh(x) integration by parts + quick reminder of sinhx coshx derivatives.
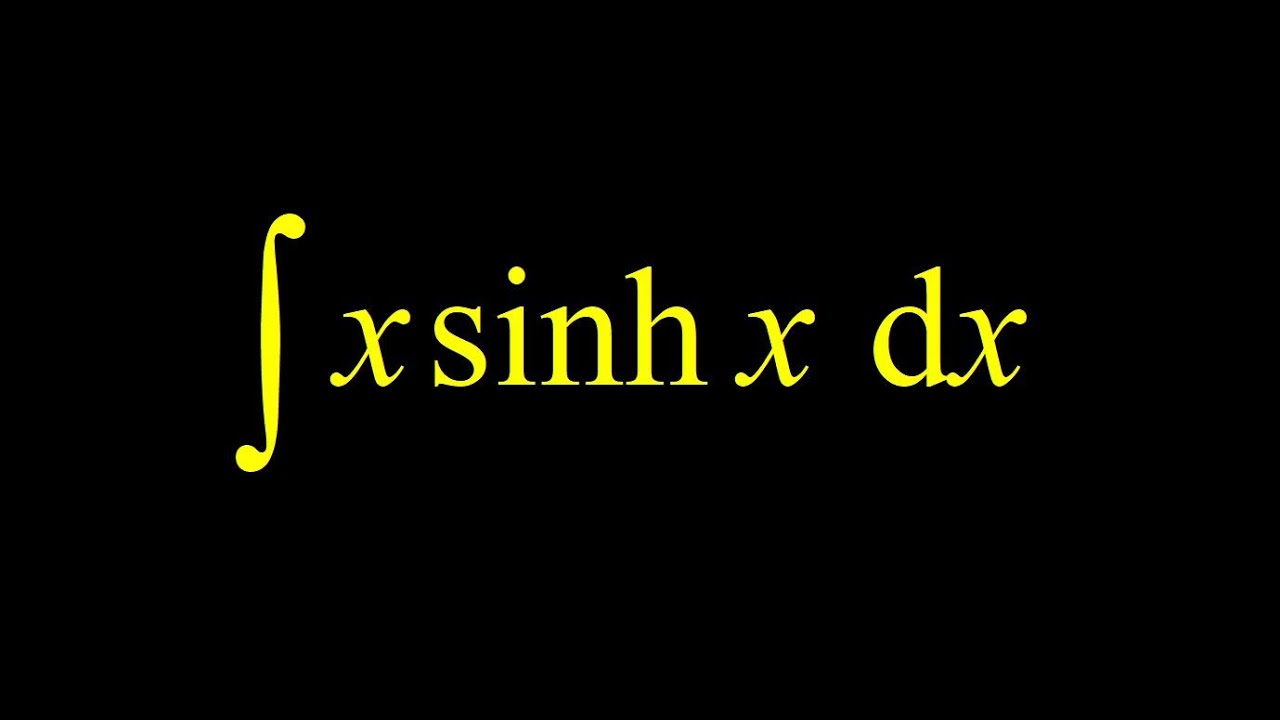
Показать описание
00:00 Introduction: we're going to compute the integral of x*sinh(x), where the sinh(x) is the hyperbolic sine function.
00:08 Reminder of sinh(x) definition, cosh(x) definition and sinhx coshx derivatives: we give a quick reminder of the definition of sinh(x) = 1/2*(e^x-e^-x) and definition of cosh(x)=1/2*(e^x+e^-x). Then we work out the derivatives of sinh(x) and cosh(x): it turns out that the derivative of sinhx is coshx and the derivative of coshx is sinhx!
01:20 x*sinh(x) integration by parts: Now we apply integration by parts to integrate x*sinh(x). Let u=x and du=dx; let dv=sinh(x)dx so v=cosh(x) (using the derivative relationship we just figured out). Using the integration by parts formula, we obtain x*cosh(x)-integral(cosh(x))dx, or xcosh(x)-sinh(x)+C, and we're done!
00:08 Reminder of sinh(x) definition, cosh(x) definition and sinhx coshx derivatives: we give a quick reminder of the definition of sinh(x) = 1/2*(e^x-e^-x) and definition of cosh(x)=1/2*(e^x+e^-x). Then we work out the derivatives of sinh(x) and cosh(x): it turns out that the derivative of sinhx is coshx and the derivative of coshx is sinhx!
01:20 x*sinh(x) integration by parts: Now we apply integration by parts to integrate x*sinh(x). Let u=x and du=dx; let dv=sinh(x)dx so v=cosh(x) (using the derivative relationship we just figured out). Using the integration by parts formula, we obtain x*cosh(x)-integral(cosh(x))dx, or xcosh(x)-sinh(x)+C, and we're done!
 0:03:17
0:03:17
 0:02:33
0:02:33
 0:01:36
0:01:36
 0:03:10
0:03:10
 0:06:23
0:06:23
 0:01:14
0:01:14
 0:27:02
0:27:02
 0:03:44
0:03:44
 0:02:14
0:02:14
 0:01:14
0:01:14
 0:00:44
0:00:44
 0:01:45
0:01:45
 0:02:48
0:02:48
 0:01:34
0:01:34
 0:05:42
0:05:42
 0:02:01
0:02:01
 0:01:35
0:01:35
 0:05:11
0:05:11
 0:00:45
0:00:45
 0:03:20
0:03:20
 0:00:56
0:00:56
 0:01:48
0:01:48
 0:02:13
0:02:13
 0:01:41
0:01:41