Dissipative State Preparation and the Dissipative Quantum Eigensolver

Toby Cubitt (University College London)
Quantum Summer Cluster Workshop

Finding ground states of quantum many-body systems is one of the most important---and one of the most notoriously difficult---problems in physics, both in scientific research and in practical applications. Indeed, we know from a complexity-theoretic perspective that all methods (quantum or classical) must necessarily fail to find the ground state efficiently in general. The ground state energy problem is already NP-hard even for classical, frustration-free, local Hamiltonians with constant spectral gap. For general quantum Hamiltonians, the problem becomes QMA-hard.

Nonetheless, as ground state problems are of such importance, and classical algorithms are often successful despite the theoretical exponential worst-case complexity, a number of quantum algorithms for the ground state problem have been proposed and studied. From quantum phase estimation-based methods, to adiabatic state preparation, to dissipative state engineering, to the variation quantum eigensolver (VQE), to quantum/probabilistic imaginary-time evolution (QITE/PITE).

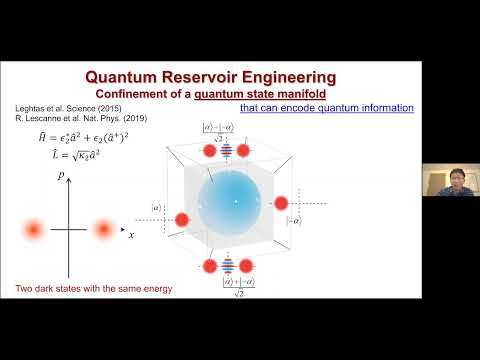
Dissipative state engineering was first introduced in 2009 by Verstraete, Cirac and Wolf and by Kraus et al. However, it only works for the restricted class of frustration-free Hamiltonians.

In this talk, I will show how to construct a dissipative state preparation dynamics that provably produces the correct ground state for arbitrary Hamiltonians, including frustrated ones. This leads to a new quantum algorithm for preparing ground states: the Dissipative Quantum Eigensolver (DQE). DQE has a number of interesting advantages over previous ground state preparation algorithms:


The entire algorithm consists simply of iterating the same set of simple local measurements repeatedly.
The expected overlap with the ground state increases monotonically with the length of time this process is allowed to run.
It converges to the ground state subspace unconditionally, without any assumptions on or prior information about the Hamiltonian (such as spectral gap or ground state energy bound).
The algorithm does not require any variational optimisation over parameters.
It is often able to find the ground state in low circuit depth in practice.
It has a simple implementation on certain types of quantum hardware, in particular photonic quantum computers.
It is immune to errors in the initial state.
It is inherently fault-resilient, without incurring any fault-tolerance overhead. I.e.\ not only is it resilient to errors on the quantum state, but also to faulty implementations of the algorithm itself; the overlap of the output with the ground state subspace degrades smoothly with the error rate, independent of the total run-time.
I give a mathematically rigorous analysis of the DQE algorithm and proofs of all the above properties, using non-commutative generalisations of methods from classical probability theory.