filmov
tv
Finding the zeros of a function - Zeros of polynomial function

Показать описание
👉 Learn how to find all the zeros of a polynomial in the form of the difference of two squares. A polynomial is an expression of the form ax^n + bx^(n-1) + . . . + k, where a, b, and k are constants and the exponents are positive integers. The zeros of a polynomial are the values of x for which the value of the polynomial is zero. A polynomial is said to be the difference of two squares if the polynomial is expressed as a difference of two terms which can be expressed as the squares of a number (or expression).
To find the zeros of a polynomial in the form of the difference of two squares, we first equate the polynomial to 0 and factor out any common factor of the two terms. We then use our knowledge of techniques of factoring the difference of two squares polynomials to factor the polynomial. After we have factored the polynomial, we can then use the zero-product property to evaluate the factored polynomial and hence obtain the zeros of the polynomial.
Recall that the zero-product property states that when the product of two or more terms is zero, then either of the term is equal to 0.
Organized Videos:
✅Zeros of a Polynomial by Factoring
✅Zeros and Multiplicity of Polynomials | Learn About
✅How to Find all of the Zeros by Sum and Difference of Two Cubes
✅How to Find all of the Zeros by Grouping
✅How to Find all of the Zeros in Factored Form
✅How to Find all of the Zeros by Factoring 5th Degree
✅How to Find all of the Zeros by Difference of Two Squares
✅How to Find all of the Zeros by Factoring 4th Degree
✅How to Find all of the Zeros of a 3rd Degree Polynomial
✅How to Find all of the Zeros Without Factoring
Connect with me:
#polynomials #brianmclogan
To find the zeros of a polynomial in the form of the difference of two squares, we first equate the polynomial to 0 and factor out any common factor of the two terms. We then use our knowledge of techniques of factoring the difference of two squares polynomials to factor the polynomial. After we have factored the polynomial, we can then use the zero-product property to evaluate the factored polynomial and hence obtain the zeros of the polynomial.
Recall that the zero-product property states that when the product of two or more terms is zero, then either of the term is equal to 0.
Organized Videos:
✅Zeros of a Polynomial by Factoring
✅Zeros and Multiplicity of Polynomials | Learn About
✅How to Find all of the Zeros by Sum and Difference of Two Cubes
✅How to Find all of the Zeros by Grouping
✅How to Find all of the Zeros in Factored Form
✅How to Find all of the Zeros by Factoring 5th Degree
✅How to Find all of the Zeros by Difference of Two Squares
✅How to Find all of the Zeros by Factoring 4th Degree
✅How to Find all of the Zeros of a 3rd Degree Polynomial
✅How to Find all of the Zeros Without Factoring
Connect with me:
#polynomials #brianmclogan
Комментарии
 0:12:18
0:12:18
 0:05:48
0:05:48
 0:02:52
0:02:52
 0:17:42
0:17:42
 0:06:07
0:06:07
 0:05:48
0:05:48
 0:03:57
0:03:57
 0:04:30
0:04:30
 0:14:48
0:14:48
 0:09:37
0:09:37
 0:02:49
0:02:49
 0:10:12
0:10:12
 0:08:00
0:08:00
 0:10:10
0:10:10
 0:05:16
0:05:16
 0:05:40
0:05:40
 0:05:35
0:05:35
 0:02:38
0:02:38
 0:04:08
0:04:08
 0:01:51
0:01:51
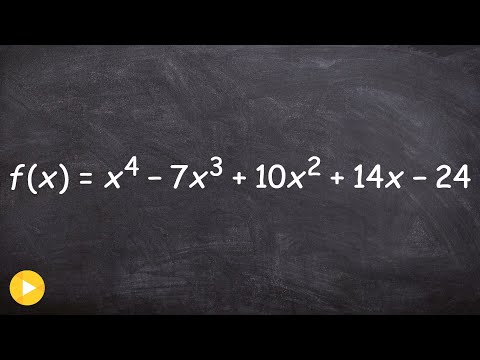 0:11:31
0:11:31
 0:06:20
0:06:20
 0:02:41
0:02:41
 0:04:08
0:04:08