filmov
tv
Linear Algebra 9g: Which Columns Are Pivot Columns in Gaussian Elimination

Показать описание
Linear Algebra 9g: Which Columns Are Pivot Columns in Gaussian Elimination
Linear Algebra - 8 - Finding the Pivot Columns
Linear Algebra 9c: Why Gaussian Elimination Works
Linear Algebra 9q: Gaussian Thinning
Row Echelon Form, Pivot Positions, Basic and Free Variables
Linear Algebra 8j: The Simplest Possible System
Pivot Positions
Pivoting
9g: Solving Ax=b with the Way of the Subspace—More examples
Linear Algebra 8f: A Tall Linear System
Linear Algebra 9e: Gaussian Elimination and Systems Without Solutions
Applied Linear Algebra, Lesson 12, Video 14: Does it Matter what pivot we choose
Linear Algebra 9c1: Gaussian Elimination Cannot Be Used to Determine the Column Space
The column space of A
Linear Algebra 9d: First Gaussian Elimination Example
Linear Algebra 9i: Gaussian Elimination Example 1
Linear Algebra 8k: You and I Have a Problem - We Need Some Distance!
01-8 Pivot positions and pivot columns
Linear Algebra 9m: Gaussian Elimination Example 5
[Linear Algebra] Echelon Form and Pivots
Linear Algebra 8p: The Relationship Between the Column Space and the Null Space
Linear Algebra 8g: A Wide Linear System
Pivots and Pivot Columns
Linear Algebra 9n: Gaussian Elimination Example 6
Комментарии
 0:10:21
0:10:21
 0:05:12
0:05:12
 0:08:27
0:08:27
 0:04:45
0:04:45
 0:08:47
0:08:47
 0:07:11
0:07:11
 0:01:36
0:01:36
 0:04:03
0:04:03
 0:21:27
0:21:27
 0:06:51
0:06:51
 0:05:57
0:05:57
 0:03:44
0:03:44
 0:01:44
0:01:44
 0:11:26
0:11:26
 0:15:33
0:15:33
 0:09:30
0:09:30
 0:05:07
0:05:07
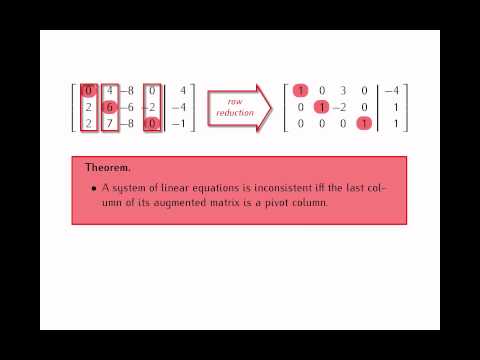 0:09:53
0:09:53
 0:02:20
0:02:20
![[Linear Algebra] Echelon](https://i.ytimg.com/vi/vfZuQoTNCN0/hqdefault.jpg) 0:09:41
0:09:41
 0:28:13
0:28:13
 0:08:18
0:08:18
 0:01:23
0:01:23
 0:04:11
0:04:11