Derivative of y=cos(xy)

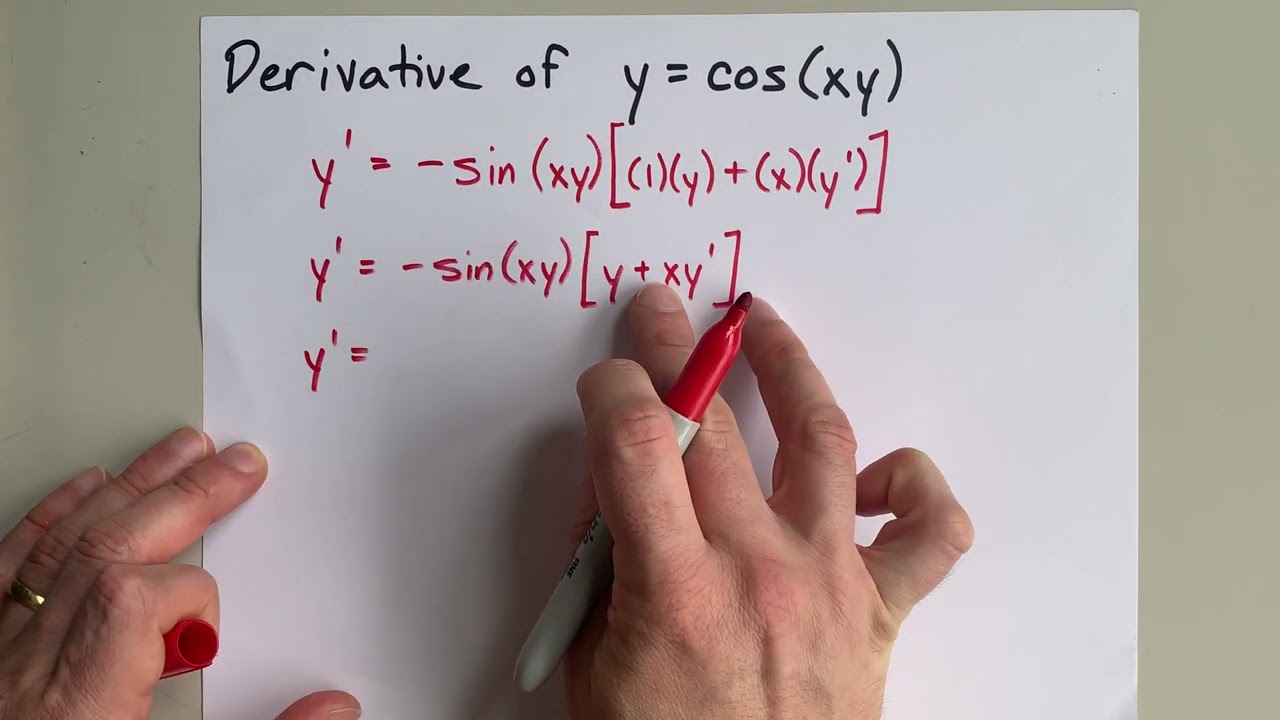
preview_player
Показать описание
To find the derivative of this function, you'll need implicit differentiation.
derivative of y is just y'
derivative of cos(xy) requires chain rule AND product rule. It's -sin(xy)*(y+xy')

After taking this derivative, you'll need to multiply the -sin(xy) through the brackets (distribute) and then collect terms that contain y' on the one side of the equation. Then factor, and isolate y' with division.
  1. mroldridge
Рекомендации по теме
Derivative of y=cos(xy) 0:03:52

Derivative of y=cos(xy)

Find derivative implicitly 0:04:29

Find derivative implicitly with respect to x for cos(xy) = 1 + sin y

How to use 0:02:38

How to use implicit differentiation with trig

If Cos(x-y) = 0:10:33

If Cos(x-y) = xe^x find dy/dx.

12th Class Derivative 0:00:22

12th Class Derivative cos(xY) = x + Y solution #shorts #derivatives #dayalsir

Implicit Differentiation || 0:04:10

Implicit Differentiation || y=cos(xy)

If ` e^(x+y) 0:03:41

If ` e^(x+y) =cos (x-y) ,then (dy)/(dx)=`

9. DERIVATIVE Find 0:06:04

9. DERIVATIVE Find dy by dx of sin2 y + cos xy = π

Partial Derivative of 0:00:44

Partial Derivative of cos(xy) w.r.t. x || Partial Differentiation #calculus #mathematics #shorts

`cos(xy)=x+y` 0:02:42

`cos(xy)=x+y`

Partial Derivative of 0:01:32

Partial Derivative of z = cos(xy)

Implicit derivative of 0:04:08

Implicit derivative of y = cos(5x - 3y) | Taking derivatives | Differential Calculus | Khan Academy

find Dxy by 0:02:19

find Dxy by implicit differentiation of cos(xy^2) = y^2 + x

Find both first 0:01:16

Find both first partial derivatives. z = \cos xy | Plainmath

Gradient of f(x,y) 0:02:10

Gradient of f(x,y) = yx^2 + cos(xy)

Implicit Differentiation: Equation 0:07:41

Implicit Differentiation: Equation of Tangent Line xy+cos(xy)-4x=-7

2 Ways to 0:06:33

2 Ways to Differentiate (sin^2(y) + cos(xy) = 1) in Implicit Differentiation Calculus

Calculus in 24 0:08:20

Calculus in 24 hours- Partial Derivatives of Cos(xy)

sin^2(y) + cos(xy) 0:03:28

sin^2(y) + cos(xy) = π Find dy/dx. Differentiation | NCERT | CalculusCheck

Implicit differentiation sin(xy)=cos(x+y) 0:07:00

Implicit differentiation sin(xy)=cos(x+y) & sin(y)+cos(x)=1

find the derivative 0:04:42

find the derivative of following equation sin^2 y + cos xy = pi

05 Ex4 - 0:02:44

05 Ex4 - Simplifying expression cos(x-y)cos(y) - sin(x-y)sin(y)

lim (x,y) approaches 0:00:44

lim (x,y) approaches (0,0) of (1-cos(xy))/xy

Find dy/dx of 0:06:20

Find dy/dx of sin2 y + cos xy = κ

Комментарии
Автор

Nice video! Just have a few observations:

a) It would be fun to write the function y as:
y = )...)




b) We can also use the multivariate chain rule to do essentially the same as what u did:

df(x, y) = (∂f/∂x) dx + (∂f/∂y) dy. In this example, with f(x, y) = cos(xy),

==> 1 = (∂f/∂x) (1/y') + (∂f/∂y) = [-ysin(xy)]/y' - xsin(xy)

==> 1/y' = [1+ xsin(xy)] / [-ysin(xy)], giving the same answer you got

adwz
Автор

Nice video ❤
I wonder, would this question be the same as asking:
Find the derivative of y for
y = cos(xcos(xcos(xcos(x…))))? Going infinitely

haidaralhassan
Автор

Should note the domain of y is relative to the x given (arccos(y)/y)=x.

Trade_Mark